
| (1)$\frac{4}{13}+({\frac{7}{13}-\frac{5}{13}})$ | (2)$\frac{7}{9}-\frac{5}{12}+\frac{5}{18}$ | (3)$\frac{11}{15}-({\frac{4}{5}-\frac{4}{3}})$ |
| (4)$2\frac{1}{3}-({\frac{1}{6}+0.75})$ | (5)3.74+$1\frac{4}{9}+2.26+1\frac{5}{9}$ | (6)$\frac{15}{14}×\frac{21}{10}÷\frac{3}{4}$. |
分析 本题要根据分数的加法、减法、乘法与除法的计算法则以及四则混合运算的运算顺序计算即可,其中“3.74+$1\frac{4}{9}+2.26+1\frac{5}{9}$”可据加法交换律及结合律进行计算.
解答 解:(1)$\frac{4}{13}+({\frac{7}{13}-\frac{5}{13}})$
=$\frac{4}{13}+\frac{2}{13}$,
=$\frac{6}{13}$;
(2)$\frac{7}{9}-\frac{5}{12}+\frac{5}{18}$
=$\frac{28}{36}-\frac{15}{36}+\frac{10}{36}$,
=$\frac{23}{36}$;
(3)$\frac{11}{15}-({\frac{4}{5}-\frac{4}{3}})$
=$\frac{11}{15}-({\frac{12}{15}-\frac{20}{15}})$,
=$\frac{11}{15}-\frac{12}{15}+\frac{20}{15}$,
=$\frac{19}{15}$;
(4)$2\frac{1}{3}-({\frac{1}{6}+0.75})$
=$2\frac{1}{3}-({\frac{1}{6}+\frac{3}{4}})$,
=$2\frac{1}{3}-({\frac{2}{12}+\frac{9}{12}})$,
=$2\frac{1}{3}$-$\frac{11}{12}$,
=$\frac{28}{12}-\frac{11}{12}$,
=$\frac{17}{12}$;
(5)3.74+$1\frac{4}{9}+2.26+1\frac{5}{9}$
=$(3.74+2.26)+({1\frac{4}{9}+1\frac{5}{9}})$,
=6+3,
=9;
(6)$\frac{15}{14}×\frac{21}{10}÷\frac{3}{4}$
=$\frac{15}{14}×\frac{21}{10}×\frac{4}{3}$,
=3.
点评 本题考查了有理数的混合运算,完成有关于分数加减法的算式时要注意通分、约分,结果要化为最简分数.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
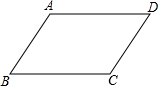 对四边形ABCD加条件,使之成为平行四边形,下面的添加不正确的是( )
对四边形ABCD加条件,使之成为平行四边形,下面的添加不正确的是( )| A. | AB=CD,AB∥CD | B. | AB∥CD,AD=BC | C. | AB=CD,AD=BC | D. | AC与BD相互平分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com