
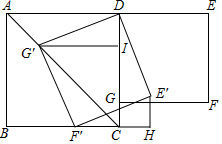
 如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )| A. | $\sqrt{2}$$+\sqrt{6}$ | B. | $\sqrt{3}+1$ | C. | $\sqrt{3}+\sqrt{2}$ | D. | $\sqrt{3}+\sqrt{6}$ |
分析 解法一:作G′I⊥CD于I,G′R⊥BC于R,E′H⊥BC交BC的延长线于H.连接RF′.则四边形RCIG′是正方形.首先证明点F′在线段BC上,再证明CH=HE′即可解决问题.
解法二:首先证明CG′+CE′=AC,作G′M⊥AD于M.解直角三角形求出DM,AM,AD即可;
解答 解法一:作G′I⊥CD于I,G′R⊥BC于R,E′H⊥BC交BC的延长线于H.连接RF′.则四边形RCIG′是正方形.
∵∠DG′F′=∠IG′R=90°,
∴∠DG′I=∠RG′F′,
在△G′ID和△G′RF中,
$\left\{\begin{array}{l}{G′D=G′F}\\{∠DG′I=∠RG′F′}\\{G′I=G′R}\end{array}\right.$,
∴△G′ID≌△G′RF,
∴∠G′ID=∠G′RF′=90°,
∴点F′在线段BC上,
在Rt△E′F′H中,∵E′F′=2,∠E′F′H=30°,
∴E′H=$\frac{1}{2}$E′F′=1,F′H=$\sqrt{3}$,
易证△RG′F′≌△HF′E′,
∴RF′=E′H,RG′=RC=F′H,
∴CH=RF′=E′H,
∴CE′=$\sqrt{2}$,
∵RG′=HF′=$\sqrt{3}$,
∴CG′=$\sqrt{2}$RG′=$\sqrt{6}$,
∴CE′+CG′=$\sqrt{2}$+$\sqrt{6}$.
故选A.
解法二:作G′M⊥AD于M.
易证△DAG'≌△DCE',
∴AG'=CE',
∴CG′+CE′=AC,
在Rt△DMG′中,∵DG′=2,∠MDG′=30°,
∴MG′=1,DM=$\sqrt{3}$,
∵∠MAG′=45°,∠AMG′=90°,
∴∠MAG′=∠MG′A=45°,
∴AM=MG′=1,
∴AD=1+$\sqrt{3}$,
∵AC=$\sqrt{2}$AD,
∴AC=$\sqrt{2}$+$\sqrt{6}$.
故选A.
点评 本题考查旋转变换、正方形的性质、全等三角形的判定和性质、勾股定理、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考选择题中的压轴题.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:选择题
 如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=3(x-3)2-3 | B. | y=3x2 | C. | y=3(x+3)2-3 | D. | y=3x2-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 70 | B. | 720 | C. | 1680 | D. | 2370 |
查看答案和解析>>
科目:初中数学 来源:2017届江苏省启东市九年级寒假作业测试(开学考试)数学试卷(解析版) 题型:填空题
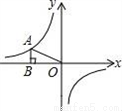
如图,点A为反比例函数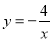 图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为 _________。
图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为 _________。
查看答案和解析>>
科目:初中数学 来源:2017届辽宁省九年级3月月考数学试卷(解析版) 题型:填空题
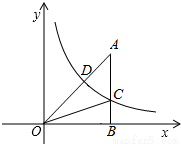
如图,反比例函数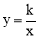 (x>0)的图象交Rt△OAB的斜边OA于点D,交直角边AB于点C,点B在x轴上.若△OAC的面积为5,AD:OD=1:2,则k的值为
(x>0)的图象交Rt△OAB的斜边OA于点D,交直角边AB于点C,点B在x轴上.若△OAC的面积为5,AD:OD=1:2,则k的值为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com