练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    方程的解为(　 　)

    A. B. C. ， D. ，

    C 【解析】试题解析： 分解因式得：x(x+1)=0， ∴x=0，x+1=0， 解方程得： 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：解答题

    小明家O，学校A和公园C的平面示意图如图所示，图上距离OA＝2cm，OC＝2.5cm.

    (1)学校A、公园C分别在小明家O的什么方向上？

    (2)若学校A到小明家O的实际距离是400m，求公园C到小明家O的实际距离．

    （1）学校A在小明家O的北偏东45°方向，公园C在小明家O的北偏西30°方向；（2）公园C到小明家O的实际距离是500m. 【解析】试题分析：(1)、根据方位的描述方法分别得出学校A和公园C的位置；(2)、首先根据学校A到小明家的图上距离和实际距离得出比例尺，然后根据比例尺和图上距离求出公园C到小明家的实际距离． 试题解析：【解析】 (1)∵∠NOA＝90°－45°＝45°，∠CON...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型：单选题

    若分式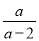有意义,则a的取值范围是(     )

    A. a≠2 B. a≠0 C. a≠2且a≠0 D. 一切实数

    A 【解析】试题解析：根据题意得：a-2≠0， 解得：a≠2． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：填空题

    若关于的一元二次方程(m-1)x2-4x+1=0有两个不相等的实数根，则m的取值范围为_____________．

    且 【解析】试题解析: ∵一元二次方程有两个不相等的实数根， ∴m?1≠0且△=16?4(m?1)>0，解得m<5且m≠1， ∴m的取值范围为m<5且m≠1. 故答案为:m<5且m≠1.

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：单选题

    若点M在抛物线的对称轴上，则点M的坐标可能是（　 　）

    A. （3，-4） B. （-3，0） C. （3，0） D. （0，-4）

    B 【解析】试题解析: ∴对称轴为x=-3， ∵点M在对称轴上, ∴M点的横坐标为-3， 故选B.

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：解答题

    如图，已知D是△ABC的边AB上一点，CE∥AB，DE交AC于点O，且OA=OC，猜想线段CD与线段AE的大小关系和位置关系，并加以证明．

    详见解析. 【解析】试题分析：根据CE∥AB，可得∠DAO=∠ECO，再由OA=OC，利用ASA可证明△ADO≌△ECO，根据全等三角形的性质可得AD=CE，再根据一组对边平行且相等的四边形是平行四边形即可判定四边形ADCE是平行四边形，由此可得出结论． 试题解析：【解析】 猜想线段CD与线段AE的大小关系和位置关系是：相等且平行． 理由：∵CE∥AB， ∴∠DAO=∠E...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：填空题

    菱形ABCD的周长为36，其相邻两内角的度数比为1：5，则此菱形的面积为 ．

    40.5 【解析】 试题分析：根据相邻两内角的度数比为1：5，可求出一个30°角，根据周长为36，求出菱形的边长，根据直角三角形里30°角的性质求出高，从而求出面积． 【解析】 作AE⊥BC于E点， ∵其相邻两内角的度数比为1：5， ∴∠B=180°×=30°， ∵菱形ABCD的周长为36， ∴AB=BC=×36=9． ∴AE=×9=． ∴菱...

    查看答案和解析>>

    科目：初中数学 来源：广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型：单选题

    若干桶方便面摆放在桌子上，如图是它的三视图，则这一堆方便面共有 _____ 桶．

    7． 【解析】试题分析：综合三视图，这堆方便面底层应该有3+1=4桶，第二层应该有2桶，第三层应该有1桶， 因此共有4+2+1=7桶． 故答案是7．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：解答题

    一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：

    售价x（元/千克）
     

    …
     

    50
     

    60
     

    70
     

    80
     

    …
     

    销售量y（千克）
     

    …
     

    100
     

    90
     

    80
     

    70
     

    …
     

    （1）求y与x的函数关系式；

    （2）该批发商若想获得4000元的利润，应将售价定为多少元？

    （3）该产品每千克售价为多少元时，批发商获得的利润w（元）最大？此时的最大利润为多少元？

    （1）y与x的函数关系式为y=-x+150；（2）该批发商若想获得4000元的利润，应将售价定为70元；（3）该产品每千克售价为85元时，批发商获得的利润w（元）最大，此时的最大利润为4225元． 【解析】试题分析：（1）根据图表中的各数可得出y与x成一次函数关系，从而结合图表的数可得出y与x的关系式． （2）根据想获得4000元的利润，列出方程求解即可； （3）根据批发商获得的...

    查看答案和解析>>

    同步练习册答案