
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
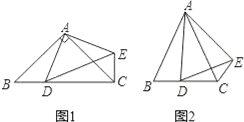
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.
【答案】(1)90°;(2)①α+β=180°,理由见解析;②当点D在射线BC上时,α+β=180°;当点D在射线BC的反向延长线上时,α=β.
【解析】(1)问要求∠BCE的度数,可将它转化成与已知角有关的联系,根据已知条件和全等三角形的判定定理,得出△ABD≌△ACE,再根据全等三角形中对应角相等,最后根据直角三角形的性质可得出结论;(2)问在第(1)问的基础上,将α+β转化成三角形的内角和;(3)问是第(1)问和第(2)问的拓展和延伸,要注意分析两种情况.
解:(1)90°.
理由:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC.
即∠BAD=∠CAE.
在△ABD与△ACE中,
AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB,
∴∠BCE=∠B+∠ACB,
又∵∠BAC=90°,
∴∠BCE=90°;
(2)①α+β=180°,
理由:∵∠BAC=∠DAE,
∴∠BAD+∠DAC=∠EAC+∠DAC.
即∠BAD=∠CAE.
在△ABD与△ACE中,
AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB.
∴∠B+∠ACB=β,
∵α+∠B+∠ACB=180°,
∴α+β=180°;
②当点D在射线BC上时,α+β=180°;
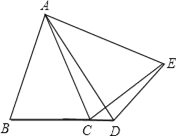
理由:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵在△ABD和△ACE中,
AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵∠BAC+∠ABD+∠BCA=180°,
∴∠BAC+∠BCE=∠BAC+∠BCA+∠ACE=∠BAC+∠BCA+∠B=180°,
∴α+β=180°;
当点D在射线BC的反向延长线上时,α=β.
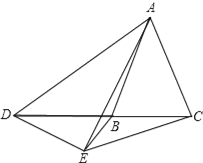
理由:∵∠DAE=∠BAC,
∴∠DAB=∠EAC,
∵在△ADB和△AEC中,
AD=AE,∠DAB=∠EAC,AB=AC,
∴△ADB≌△AEC(SAS),
∴∠ABD=∠ACE,
∵∠ABD=∠BAC+∠ACB,∠ACE=∠BCE+∠ACB,
∴∠BAC=∠BCE,
即α=β.
“点睛”本题考查三角形全等的判定,以及全等三角形的性质;两者综合运用,促进角与角相互转换,将未知角转化为已知角是关键.本题的亮点是由特例引出一般情况.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )
![]()
A. ﹣74 B. ﹣77 C. ﹣80 D .﹣83
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断( )
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150﹣180之间;
④该市居民家庭年用水量的平均数不超过180.
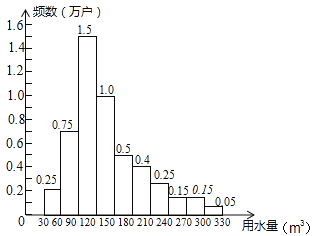
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把函数y=﹣2x+3的图象向下平移4个单位后的函数图象的解析式为( )
A.y=﹣2x+7B.y=﹣6x+3C.y=﹣2x﹣1D.y=﹣2x﹣5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com