
分析 先求出不等式组中每个不等式的解集,然后求出其公共解集,最后求其整数解进而求得b的取值范围.
解答 解:不等式组$\left\{\begin{array}{l}{x-a<0}\\{5-2x<1}\end{array}\right.$
的解集为2<x<a,
∵不等式组$\left\{\begin{array}{l}{x-a<0}\\{5-2x<1}\end{array}\right.$的整数解共有4个,为3,4,5,6;
∴6<a≤7.
故答案为:6<a≤7.
点评 此题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.


科目:初中数学 来源: 题型:解答题
 已知二次函数h=x2-(2m-1)x+m2-m(m是常数,且m≠0)
已知二次函数h=x2-(2m-1)x+m2-m(m是常数,且m≠0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
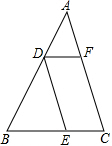 如图,在锐角三角形纸片ABC中,AC>BC,点D,E,F分别在边AB,BC,CA上,已知:DE∥AC,DF∥BC.
如图,在锐角三角形纸片ABC中,AC>BC,点D,E,F分别在边AB,BC,CA上,已知:DE∥AC,DF∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
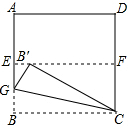 如图,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展开,然后沿直线CG折叠,使B点落在EF上,对应点为B′
如图,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展开,然后沿直线CG折叠,使B点落在EF上,对应点为B′查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )
如图,在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )| A. | 0条 | B. | 1条 | C. | 2条 | D. | 无数条 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
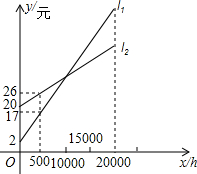 如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图象,
如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图象,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2ab+1)厘米 | B. | 8a2b厘米 | C. | (4ab+2)厘米 | D. | (4a2b-2a)厘米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com