
分析 (1)根据方程的系数结合根的判别式,即可得出△=4k2+9>0,由此即可证出此方程总有两个不相等的实数根;
(2)将x=0代入原方程,即可得出关于k的一元一次方程,解之即可得出k的值.
解答 (1)证明:在方程x2+(2k-3)x-3k=0中,△=b2-4ac=(2k-3)2-4×(-3k)=4k2-12k+9+12k=4k2+9>0,
∴此方程总有两个不相等的实数根.
(2)解:将x=0代入x2+(2k-3)x-3k=0中,
-3k=0,解得:k=0.
∴如果方程有一个根为0,k的值为0.
点评 本题考查了根的判别式以及一元二次方程的解,解题的关键是:(1)牢记“当△>0时,方程有两个不相等的实数根”;(2)将x=0代入原方程求出k值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是某游乐城的平面示意图,如图用(8,2)表示入口处的位置,用(6,-1)表示球幕电影的位置,那么坐标原点表示的位置是( )
如图是某游乐城的平面示意图,如图用(8,2)表示入口处的位置,用(6,-1)表示球幕电影的位置,那么坐标原点表示的位置是( )| A. | 太空秋千 | B. | 梦幻艺馆 | C. | 海底世界 | D. | 激光战车 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
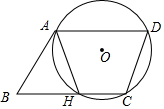 如图,⊙O过?ABCD的顶点A,D,C,边AB与⊙O相切于点A,边BC与⊙O相交于点H.
如图,⊙O过?ABCD的顶点A,D,C,边AB与⊙O相切于点A,边BC与⊙O相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
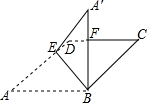 如图,有一张菱形纸片ABCD,∠C=40°,BC=4cm,E为边AD上的点.将△ABE沿BE折叠得到△A′BE,A′B交CD于点F.当A′B⊥CD时,求线段A′F的长.(结果精确到0.1cm)
如图,有一张菱形纸片ABCD,∠C=40°,BC=4cm,E为边AD上的点.将△ABE沿BE折叠得到△A′BE,A′B交CD于点F.当A′B⊥CD时,求线段A′F的长.(结果精确到0.1cm)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com