
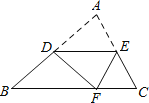
【题目】如图,在△ABC中,∠A=70°∠B=50°,点D,E分别为AB,AC上的点,沿DE折叠,使点A落在BC边上点F处,若△EFC为直角三角形,则∠BDF的度数为______.
【答案】110°或50°.
【解析】
由内角和定理得出∠C=60°,根据翻折变换的性质知∠DFE=∠A=70°,再分∠EFC=90°和∠FEC=90°两种情况,先求出∠DFC度数,继而由∠BDF=∠DFC﹣∠B可得答案.
∵△ABC中,∠A=70°、∠B=50°,∴∠C=180°﹣∠A﹣∠B=60°,由翻折性质知∠DFE=∠A=70°,分两种情况讨论:
①当∠EFC=90°时,∠DFC=∠DFE+∠EFC=160°,则∠BDF=∠DFC﹣∠B=110°;
②当∠FEC=90°时,∠EFC=180°﹣∠FEC﹣∠C=30°,∴∠DFC=∠DFE+∠EFC=100°,∠BDF=∠DFC﹣∠B=50°;
综上:∠BDF的度数为110°或50°.
故答案为:110°或50°.


科目:初中数学 来源: 题型:
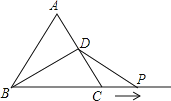
【题目】如图,等边△ABC的边长为10cm,点D是边AC的中点,动点P从点C出发,沿BC的延长线以2cm/s的速度做匀速运动,设点P的运动时间为t(秒),若△BDP是等腰三角形,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某房产开发公司对一幢住宅楼的标价是:基价2580元/平方米,楼层差价如下表:

老王买了面积为80平方米的三楼.
(1)问老王花了多少钱?
(2)若他用同样多的钱去买六楼,请你帮老王算一算他可以多买多少平方米的房子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A,B,C,D,E五个整数点(即各点均表示整数),且AB=2BC=3CD=4DE,若A、E两点表示的数的分别为-13和12,那么,该数轴上上述五个点所表示的整数中,离线段AE的中点最近的整数是( )
![]()
A. -1 B. 5 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护视力要求人写字时眼睛和笔端的距离应超过30cm,图1是一位同学的坐姿,把他的眼睛B,肘关节C和笔端A的位置关系抽象成图2的△ABC,已知BC=30cm,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3) 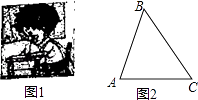
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解本校七年级700名学生上学期参加社会实践活动的时间,随机对该年级50名学生进行了调查.根据收集的数据绘制了频数分布直方图,则以下说法正确的是( )
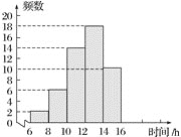
A. 学生参加社会实践活动时间最多的是16 h
B. 学生参加社会实践活动的时间大多数是12~14 h
C. 学生参加社会实践活动时间不少于10 h的为84%
D. 由样本可以估计全年级700人中参加社会实践活动时间为6~8 h的大约有26人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情景:
如图,在直角坐标系xOy中,点A、B为二次函数y=ax2(a>0)图象上的两点,且点A、B的横坐标分别为m、n(m>n>0),连接OA、AB、OB.设△AOB的面积为S时,解答下列问题: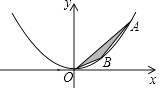
(1)探究:当a=1时,
mn | m﹣n | S | |
m=3,n=1 | 3 | 2 | |
m=5,n=2 | 10 | 3 |
当a=2时,
2mn | m﹣n | S | |
m=3,n=1 | 6 | 2 | |
m=5,n=2 | 20 | 3 |
(2)归纳证明:对任意m、n(m>n>0),猜想S=(用a,m,n表示),并证明你的猜想.
(3)拓展应用:
若点A、B的横坐标分别为m、n(m>0>n),其它条件不变时,△AOB的面积S=(用a,m,n表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,H是边BC的中点,连接 DH与 BE相交于点 G,若GE=3,则BF=_____.
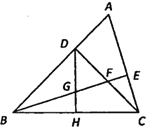
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为 1,CD⊥AB 于点 D,E 为射线 CD 上一点,以BE为边在 BE 左侧作等边△BEF,则DF的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com