
 连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )
连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )| A. | $\frac{1}{2004}$ | B. | ${(\frac{1}{2})^{2016}}$ | C. | ${(\frac{1}{4})^{2016}}$ | D. | $1-{(\frac{1}{4})^{2016}}$ |
分析 先计算出边长为1的正方形的面积为12=1,再观察图形通过计算得第1次操作后右下角的小正方形面积=$\frac{1}{4}$,第2次操作后右下角的小正方形面积=$\frac{1}{4}$×$\frac{1}{4}$=($\frac{1}{4}$)2,第3次操作后右下角的小正方形面积=($\frac{1}{4}$)3,…,则第n次操作后右下角的小正方形面积=($\frac{1}{4}$)n,然后把n=2016代入即可.
解答 解:边长为1的正方形的面积为12=1,
∵第1次操作后右下角的小正方形面积=$\frac{1}{4}$,
第2次操作后右下角的小正方形面积=$\frac{1}{4}$×$\frac{1}{4}$=($\frac{1}{4}$)2,
第3次操作后右下角的小正方形面积=($\frac{1}{4}$)3,
…
∴第2016次操作后右下角的小正方形面积=($\frac{1}{4}$)2016.
故选C.
点评 本题考查了规律型:图形的变化类:通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
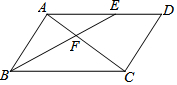 如图,在?ABCD中,BC=5,AB=3,BE平分∠ABC交AD于点E,交对角线AC于点F,则$\frac{{{S_{△AEF}}}}{{{S_{△CBF}}}}$=$\frac{9}{25}$.
如图,在?ABCD中,BC=5,AB=3,BE平分∠ABC交AD于点E,交对角线AC于点F,则$\frac{{{S_{△AEF}}}}{{{S_{△CBF}}}}$=$\frac{9}{25}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
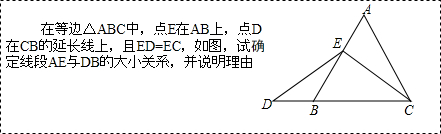
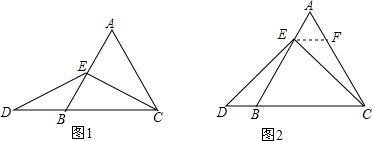
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
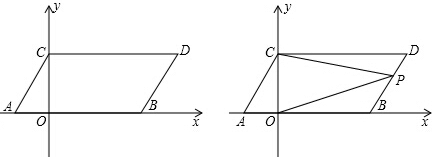
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com