
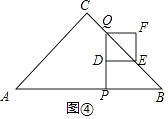
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬��A=45�㣬AB=4cm����P�ӵ�A��������2cm/s���ٶ��ر�AB���յ�B�˶�������P��PQ��AB������ACB�ڵ�Q��DΪPQ�е㣬��DQΪ�����Ҳ���������DEFQ����������DEFQ���ABC�ص�����ͼ�ε������y��cm2������P���˶�ʱ��Ϊx��s����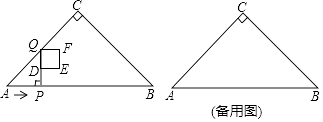
��1������Q�ڱ�AC��ʱ��������DEFQ�ı߳�Ϊcm���ú�x�Ĵ���ʽ��ʾ����
��2������P�����B�غ�ʱ�����F���ڱ�BC��ʱx��ֵ��
��3����0��x��2ʱ����y����x�ĺ�������ʽ��
��4��ֱ��д����BC���е�����������DEFQ�ڲ�ʱx��ȡֵ��Χ��
���𰸡�
��1��x
��2���⣺��ͼ�٣��ӳ�FE��AB��G���������AP=2x��
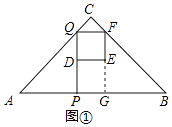
��DΪPQ�е㣬
��DQ=x��
��GP=x��
��2x+x+2x=4��
��x= ![]() ��
��
��3���⣺��ͼ�ڣ���0��x�� ![]() ʱ��y=S������DEFQ=DQ2=x2��
ʱ��y=S������DEFQ=DQ2=x2��
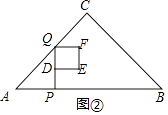
��y=x2��
��ͼ�ۣ��� ![]() ��x��1ʱ����C��CH��AB��H����FQ��K����CH=
��x��1ʱ����C��CH��AB��H����FQ��K����CH= ![]() AB=2��
AB=2��
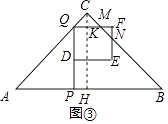
��PQ=AP=2x��CK=2��2x��
��MQ=2CK=4��4x��FM=x����4��4x��=5x��4��
��y=S������DEFQ��S��MNF=DQ2�� ![]() FM2��
FM2��
��y=x2�� ![]() ��5x��4��2=��
��5x��4��2=�� ![]() x2+20x��8��
x2+20x��8��
��y=�� ![]() x2+20x��8��
x2+20x��8��
��ͼ�ܣ���1��x��2ʱ��PQ=4��2x��
��DQ=2��x��
��y=S��DEQ= ![]() DQ2��
DQ2��
��y= ![]() ��2��x��2��
��2��x��2��
��y= ![]() x2��2x+2��
x2��2x+2��
��4���⣺��Q��C�غ�ʱ��EΪBC���е㣬
��2x=2��
��x=1��
��QΪBC���е�ʱ��BQ= ![]() ��
��
PB=1��
��AP=3��
��2x=3��
��x= ![]() ��
��
���BC���е�����������DEFQ�ڲ�ʱx��ȡֵ��ΧΪ��1��x�� ![]() ��
��
����������1���ߡ�ACB=90�㣬��A=45�㣬PQ��AB��
���AQP=45�㣬
��PQ=AP=2x��
��DΪPQ�е㣬
��DQ=x��
���Դ��ǣ�x��
��2��������⣬����ʾ��ͼ��FG=BG=2x,PQ=AP=2x,��AB=x+2x+2x�������̣����x����3���ɵڣ�2����Ϊ������x=![]() �Ƿֽ�㣬�ֶ�����ʱ�ͷ�Ϊ0��x��
�Ƿֽ�㣬�ֶ�����ʱ�ͷ�Ϊ0��x�� ![]() ��
�� ![]() ��x��1��1��x��2����4���ȼ����е����������ε���������Ϊ���㣬�ֱ��������ʱ��Ӧ��xֵ�����������Χ.
��x��1��1��x��2����4���ȼ����е����������ε���������Ϊ���㣬�ֱ��������ʱ��Ӧ��xֵ�����������Χ.
�����㾫����������Ҫ�����˺�����ϵʽ�ͺ����Ա�����ȡֵ��Χ�����֪ʶ�㣬��Ҫ����������ʾ������ϵ����ѧʽ�ӽ�����������ʽ������ϵʽ��ʹ������������Ա�����ȡֵ��ȫ�壬�����Ա�����ȡֵ��Χ������ȷ�����⣮


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ƽ���ı���ABCD�У���E��F��G��H�ֱ��ڱ�AB��BC��CD��DA�ϣ�AE=CG��AH=CF����EGƽ�֡�HEF����֤��
��1����AEH�ա�CGF��
��2���ı���EFGH�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����������������ʼ�����xֵΪ100�����Ƿ��ֵ�1������Ľ��Ϊ50����2������Ľ��Ϊ25��������2018������Ľ��Ϊ_________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��1�����㣺�� ![]() ��2��0������1��2017+
��2��0������1��2017+ ![]() ��sin45�㣻
��sin45�㣻
��2������ ![]() ��
�� ![]() ����
���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˴ٽ�ѧ����������չ��ijУ��֯��չ�����Ż���ֱ������������ࡢ�����ࡢ��ѧ�༰���������ţ�Ҫ�����˲������ţ�ÿ��ֻ��ѡ��һ���Ϊ�˽�ѧ��ϲ���������Ż��ѧУ����һ�γ������飮�����ռ��������ݣ����Ƴ�����������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺ 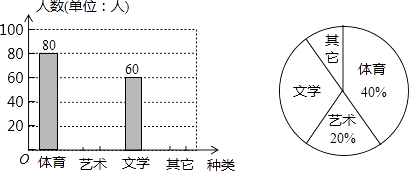
��1���˴ι������˶����ˣ�
��2������ѧ����������ͳ��ͼ����ռԲ�ĽǵĶ�����
��3���뽫����ͳ��ͼ����������
��4������У��1500��ѧ���������ϲ�����������ŵ�ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��ij����B��ij��ͬʱ�Ƴɻ�������̨��A��ij����֧Ԯ���10̨��B��ij����֧Ԯ���4̨���־�����C��8̨��D��6̨����֪��A����D��C���ص��˷ѷֱ���200Ԫÿ̨��400Ԫÿ̨����B����D��C���ص��˷ѷֱ���150Ԫÿ̨��250Ԫÿ̨��
��1����B��ij������D��x̨�������˷�Ϊ����Ԫ��
��2���ڣ�1���У���x��2ʱ�����˷��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������3000Ԫ����ij�ָɹ����ۣ���������״�����ã������ֵ���9000Ԫ�ʽ����ָɹ�������εĽ��۱ȵ�һ�εĽ��������20%�������ɹ������ǵ�һ�ε�2������300ǧ�ˣ�������а�ÿǧ��9Ԫ�ļ۸���ۣ����ָɹ��۳������µ�600ǧ�˰��ۼ۵�8�����꣮
��1�����ָɹ��ĵ�һ�ν�����ÿǧ�˶���Ԫ��
��2�������������ָɹ���ӯ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ݵIJ�����ǽ�ڵ���״��ͼ��ʾ�����ɵ���������OCD�;���ABCD��ɣ���OCD=25�㣬��ǽ������Ϳ��Ϳ����ɫ��ͬ�����ƣ�����һ�����״���ı���EFGH�����FG��EH��GH=2.6m����FGB=65�㣮
��1����֤��GF��OC��
��2����EF�ij��������ȷ��0.1m����
���ο����ݣ�sin25��=cos65���0.42��cos25��=sin65���0.91��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���ڸ�����������������ȡ�Ա���x��һ��ֵ����x��0ʱ�����Ƕ�Ӧ�ĺ���ֵ��Ϊ�෴������x��0ʱ�����Ƕ�Ӧ�ĺ���ֵ��ȣ����dz�����������������Ϊ��غ��������磺һ�κ���y=x��1��������غ���Ϊy= ![]() ��
��
��1����֪��A����5��8����һ�κ���y=ax��3����غ�����ͼ���ϣ���a��ֵ��
��2����֪���κ���y=��x2+4x�� ![]() ���ٵ���B��m��
���ٵ���B��m�� ![]() ���������������غ�����ͼ����ʱ����m��ֵ��
���������������غ�����ͼ����ʱ����m��ֵ��
�ڵ���3��x��3ʱ������y=��x2+4x�� ![]() ����غ��������ֵ����Сֵ��
����غ��������ֵ����Сֵ��
��3����ƽ��ֱ������ϵ�У���M��N������ֱ�Ϊ���� ![]() ��1������
��1������ ![]() ��1��������MN��ֱ��д���߶�MN���
��1��������MN��ֱ��д���߶�MN���
�κ���y=��x2+4x+n����غ�����ͼ��������������ʱn��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com