练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    元旦期间，某商场设置了如图所示的幸运转盘，转盘分成4个大小相同的扇形，分别标有数学1，2，3，4，指针的位置固定，转盘可以自由转动，当转动的转盘停止后，其中的某个扇形会停在指针所指的位置（指针指向两个扇形的交线时，当作右边的扇形）．商场规定：凡是参加抽奖的顾客均可转动转盘两次，如果两次转动中指针指缶扇形上的数字之和为8是一等奖，数字之和为7是二等奖，数字之和为6是三等奖，标号之和为其他数字则获得一份纪念品，请分别求出顾客抽中一、二、三等奖的概率．

    【解析】试题分析：画树状图展示所有16种等可能出现的结果数，再找出转出的两个数字之和为8的结果数、数字之和为7的结果数和数字之和为6的结果数，然后根据概率公式求解． 试题解析： 【解析】 画出树状图为： 由树状图可以看出，所有可能出现的结果共有16种，并且每种结果出现的可能性都相等．其中转出的两个数字之和为8的结果有1种，数字之和为7的结果有2种，数字之和为6的结果有3种， ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十七章达标检测卷 题型：解答题

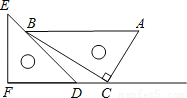
    一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，AC=10，试求CD的长．

    15﹣5． 【解析】 试题分析：过点B作BM⊥FD于点M，根据题意可求出BC的长度，然后在△EFD中可求出∠EDF=45°，进而可得出答案． 【解析】 过点B作BM⊥FD于点M， 在△ACB中，∠ACB=90°，∠A=60°，AC=10， ∴∠ABC=30°，BC=AC×tan60°=10， ∵AB∥CF， ∴BM=BC×sin30°=10×=5， ...

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型：单选题

    一元二次方程x2﹣6x﹣5=0配方可变形为（　　）

    A. （x﹣3）2=14 B. （x﹣3）2=4 C. （x+3）2=14 D. （x+3）2=4

    A 【解析】试题分析：x2﹣6x﹣5=0，把方程的常数项移到右边得，x2﹣6x=5，方程两边都加上32得，x2﹣6x+9=5+9，所以（x﹣3）2=14，故答案选C.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版七年级数学上册：第5章 一元一次方程 单元测试卷 题型：单选题

    方程－2x＋3＝0的解是(　　)

    A. x＝ B. x＝－ C. x＝ D. x＝－

    C 【解析】【解析】 移项得：－2x＝－3，系数化为1得： ．故选C．

    查看答案和解析>>

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：解答题

    综合与探究

    如图，在平面直角坐标系xOy中，抛物线W的函数表达式为y=﹣x2+2x+3，抛物线W与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C，它的顶点为D，直线l经过A、C两点．

    （1）求点A、B、C、D的坐标．

    （2）将直线l向下平移m个单位，对应的直线为l′．

    ①若直线l′与x轴的正半轴交于点E，与y轴的正半轴交于点F，△AEF的面积为S，求S关于m的函数关系式，并写出自变量m的取值范围；

    ②求m的值为多少时，S的值最大？最大值为多少？

    （3）若将抛物线W也向下平移m单位，再向右平移1个单位，使平移后得到的二次函数图象的顶点P落在△AOC的内部（不包括△AOC的边界），请直接写出m的取值范围．

    （1）点D坐标为（1，4）（2）①S=﹣m2+m（0＜m＜3），②当m=时，S的值最大，最大值为（3）3＜m＜4 【解析】试题分析：（1）令y＝0，求出A，B的横坐标，令x＝0求出C的纵坐标，把二次函数解析式转化为顶点式即可得出D的坐标； （2）①利用待定系数法确定出直线l的解析式，根据平移得出l′的解析式，求出与坐标轴的交点E，F的坐标，得出AE，OF的长，最后用面积公式即可得出结论...

    查看答案和解析>>

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：填空题

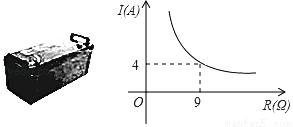
    如图所示蓄电池的电压为定值，使用该蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示，如果以此蓄电池为电源的电器的限制电流不超过12A，那么用电器可变电阻R应控制的范围是_____．

    R≥3 【解析】试题分析：设电流I与电阻R的函数关系式为I＝， ∵图象经过的点（9，4）， ∴k＝36， ∴I＝， k＝36＞0，在每一个象限内，I随R的增大而减小， ∴当I取得最大值12时，R取得最小值＝3， ∴R≥3， 故答案为：R≥3．

    查看答案和解析>>

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：单选题

    已知二次函数y=ax2+bx+c的x、y的部分对应值如下表：

    X

    …

    ﹣1

    0

    1

    2

    3

    …

    y

    …

    5

    1

    ﹣1

    ﹣1

    1

    …

    则该函数的对称轴为（　　）

    A. y轴 B. 直线x=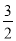 C. 直线x=2 D. 直线x=

    B 【解析】试题分析：∵x＝1和2时的函数值都是－1， ∴对称轴为直线x＝＝． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省大庆市杜尔伯特县九年级（上）期末数学试卷（五四学制） 题型：填空题

    如图，在⊙O中，弦AB=8，M是弦AB上的动点，且OM的最小值为3．则⊙O的半径为_____．

    5 【解析】试题解析:根据垂线段最短知，当OM⊥AB时，OM有最小值， 此时，由垂径定理知，点M是AB的中点， 连接OA，AM=AB=4， 由勾股定理知，OA2=OM2+AM2． 即OA2=42+32， 解得OA=5． 所以⊙O的半径为5； 故答案为5．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型：解答题

    如图，已知Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线分别交BC、CD于E、F.试说明△CEF是等腰三角形.

    说明见解析. 【解析】试题分析：要证明△CEF是等腰三角形，需证明有两角相等即可。利用角平分线、直角三角形及三角形外角的性质，进行等量代换，可求证。 【解析】 ∵∠ACB＝90°， ∴∠B＋∠BAC＝90°. ∵CD⊥AB， ∴∠CAD＋∠ACD＝90°.∴∠ACD＝∠B. ∵AE是∠BAC的平分线，∴∠CAE＝∠EAB. ∵∠EAB＋∠B＝∠CEA，∠...

    查看答案和解析>>

    同步练习册答案