
【题目】在平面直角坐标系中,对于点P(m,n)和点Q(x,y).给出如下定义:若![]() ,则称点Q为点P的“伴随点”.例如:点(1,2)的“伴随点”为点(5,0).
,则称点Q为点P的“伴随点”.例如:点(1,2)的“伴随点”为点(5,0).
(1)若点Q(﹣2,﹣4)是一次函数y=kx+2图象上点P的“伴随点”,求k的值.
(2)已知点P(m,n)在抛物线C1:y=![]() 上,设点P的“伴随点”Q(x,y)的运动轨迹为C2.
上,设点P的“伴随点”Q(x,y)的运动轨迹为C2.
①直接写出C2对应的函数关系式.
②抛物线C1的顶点为A,与x轴的交点为B(非原点),试判断在x轴上是否存在点M,使得以A、B、Q、M为顶点的四边形是平行四边形?若存在,求点M的坐标;若不存在,说明理由.
③若点P的横坐标满足﹣2≤m≤a时,点Q的纵坐标y满足﹣3≤y≤1,直接写出a的取值范围.
【答案】(1)![]() ;(2) ①y=
;(2) ①y=![]() x2﹣3x+6;②见解析;③2≤a≤6.
x2﹣3x+6;②见解析;③2≤a≤6.
【解析】
(1)根据伴随点定义可求k的值
(2)①根据伴随点的定义可求C2的解析式
②先求A,B坐标,以A、B、Q、M为顶点的四边形是平行四边形,则分三类讨论,根据平行四边形的性质可求M点坐标
③由x=m+4可得 2≤x≤a+4,且抛物线顶点坐标为(6,﹣3),﹣3≤y≤1可得6≤a+4≤10,可求a的取值范围.
解(1)设P(x,kx+2)
根据题意得:![]()
解得:![]()
(2)①根据题意可得
∴![]()
∴C2的解析式:![]() ,
,
②∵抛物线C1:![]()
∴B(4,0),A(2,﹣1)
∵以A、B、Q、M为顶点的四边形是平行四边形
∴若BA为边,BM为边,则AB∥MQ,AQ∥BM
∴Q与A的纵坐标相同
∴![]()
∴![]()
解得:![]()
∴![]() 或
或![]() ,
,
∵AQ=BM,A(4,0)
∴![]() 或
或![]() ,
,
若AB为边,BM为对角线,
∴对角线AQ与BM互相平分且交点在x轴上
∴Q点纵坐标为1
∴![]()
解得x1=2,x2=10
∴AQ中点横坐标为6或2,且AQ与BM互相平分
∴M(8,0)或(0,0)
若BM为边,AB为对角线,
∴AB的中点![]() 且AB与MQ互相平分
且AB与MQ互相平分
∴Q![]() 或
或![]()
∵MQ的中点为![]() ,
,
∴M![]() 或
或![]() ,
,
∴综上所述M![]() 或
或![]() ,(0,0),( 8,0)
,(0,0),( 8,0)
![]() ,
,![]() .
.
③∵x=m+4,﹣2≤m≤a
∴2≤x≤4+a
∵C2的解析式:![]()
∴顶点坐标为(6,﹣3)
∵﹣3≤y≤1
∴当y=1时,x=2或10
∴6≤4+a≤10
∴2≤a≤6.


科目:初中数学 来源: 题型:
【题目】将函数y=x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=|x+b|(b为常数)的图象
(1)当b=0时,在同一直角坐标系中分别画出函数![]() 与y=|x+b|的图象,并利用这两个图象回答:x取什么值时,
与y=|x+b|的图象,并利用这两个图象回答:x取什么值时,![]() 比|x|大?
比|x|大?
(2)若函数y=|x+b|(b为常数)的图象在直线y=1下方的点的横坐标x满足0<x<3,直接写出b的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线PT与⊙O相交于点T,直线PO与⊙O相交于A,B两点.已知∠PTA=∠B.
(1)求证:PT是⊙O的切线;
(2)若PT=6,PA=4,求⊙O的半径;
(3)若PT=TB=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
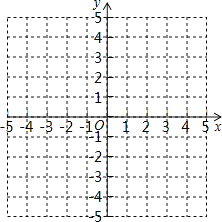
【题目】如图,在平面直角坐标系中,抛物线y=m(x+3)2+n与y=m(x﹣2)2+n+1交于点A.过点A作x轴的平行线,分别交两条抛物线于点B、C(点B在点C左侧),则线段BC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料,每瓶进价为10元.经市场调查表明,当售价在12元到14元之间(含12元,14元)浮动时,日均销售y(瓶)与售价x(元)之间的关系可近似的看作一次函数,且当x=10时,y=500;x=12,y=400.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)应将售价定为每瓶多少元时,所得日均毛利润最大?最大日均毛利润为多少元?(每瓶毛利润=每瓶售价﹣每瓶进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
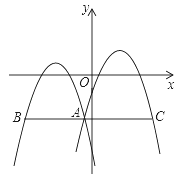
【题目】如图,已知方格纸中的每个小方格都是相同的正方形(边长为1),方格纸上有一个角∠AOB,A,O,B均为格点,请回答问题并只用无刻度直尺和铅笔,完成下列作图并简要说明画法:
(1)OA=_____;
(2)作出∠AOB的平分线并在其上标出一个点Q,使OQ=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边△ABC内一点,且PA=6,PC=8,PB=10,若△APB绕点A逆时针旋转60°后,得到△AP′C,则∠APC=_____°.
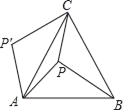
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com