
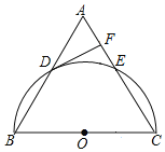
【题目】如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F
(1)判断DF与⊙O的位置关系,并证明你的结论;
(2)若DF=3,EF=1,求弦EC的长.
【答案】(1)DF与⊙O相切;(2)8.
【解析】(1)连接OD,证明OD∥AC,即可证得∠ODF=∠AFD=90°,从而证得OD是圆的切线;
(2) (2)过O作OG⊥EC交EC于点G,先证明四边形ODFG是矩形,可得:OG=3,连接OE,设半径为r,则OD=FG=OE=r, EG=r-1,由OG⊥EC可得:![]() ,即
,即![]() ,解得r=5,从而求得EC=8.
,解得r=5,从而求得EC=8.
(1)DF与⊙O相切.
连接OD.
∵AC=BC,OB=OD,
∴∠B=∠A,∠B=∠1.
∴∠A=∠1.
∴OD∥AC.
∵DF⊥AC,
∴∠AFD=90°.
∴∠ODF=∠AFD=90°.
又∵OD是⊙O的半径,
∴DF与⊙O相切.
(2)过O作OG⊥EC交EC于点G.

∵∠ODF=∠AFD=90°,
∴四边形OGFD是矩形.
∴DF=OG,OD=FG
∵DF=3,
∴OG=3
连接OE,
设半径为r,则OD=FG=OE=r
∵EF=1
∴EG=r-1
∵OG⊥EC,
∴![]()
∴![]()
∴r=5
∴EG=4
∵OG⊥EC,
∴EG=CG
∴EC=8.


科目:初中数学 来源: 题型:
【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°,其中正确的结论有( )个

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在“元旦”期间对顾客实行优惠,规定一次性购物优惠办法:
少于200元,不予优惠;高于200元但低于500元时,九折优惠;消费500元或超过500元时,其中500元部分给予九折优惠,超过500元部分给予八折优惠.根据优惠条件完成下列任务:
(1)王老师一次性购物600元,他实际付款多少元?
(2)若顾客在该超市一次性购物x元,当x小于500但不小于200时,他实际付款0.9x,当x大于或等于500元时,他实际付款多少元?(用含x的代数式表示)
(3)如果王老师两次购物货款合计820元,第一次购物的货款为a元(200<a<300),用含a的式子表示王老师两次购物实际付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
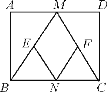
【题目】如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB与AD满足什么条件时,四边形MENF是正方形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与A、O重合)的一个动点,过点P作PE⊥PB且PE交边CD于点E.
(1)求证:PB=PE;
(2)过点E作EF⊥AC于点F,如图2.若正方形ABCD的边长为2,则在点P运动的过程中,PF的长度是否发生变化?若不变,请直接写出这个不变的值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了 h;
(2)求线段DE对应的函数解析式;
(3)求轿车从甲地出发后经过多长时间追上货车.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com