
����Ŀ����ͼ1��ʾ����������ABCD��������CGEF�У���B��C��G��ͬһ��ֱ���ϣ�M���߶�AE���е㣬DM���ӳ��߽�EF�ڵ�N������FM����֤��DM=FM��DM��FM������д֤�����̣�
��1����ͼ2������B��C��F��ͬһ��ֱ���ϣ�DM���ӳ��߽�EG�ڵ�N�������������䣬��̽���߶�DM��FM�������Ĺ�ϵ����д�����룬������֤����
��2��
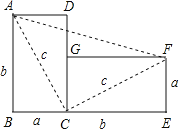
��ͼ3������E��B��C��ͬһ��ֱ���ϣ�DM���ӳ��߽�CE���ӳ����ڵ�N�������������䣬̽���߶�DM��FM�������Ĺ�ϵ����ֱ��д�����룮
���𰸡�
��1��
�⣺��ͼ2��
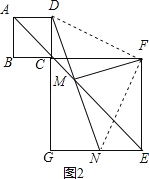
DM=FM��DM��FM��
֤��������DF��NF��
���ı���ABCD��CGEF�������Σ�
��AD��BC��BC��GE��
��AD��GE��
���DAM=��NEM��
��M��AE���е㣬
��AM=EM��
�ڡ�MAD���MEN�У�
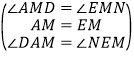
���MAD�ա�MEN��
��DM=MN��AD=EN��
��AD=CD��
��CD=NE��
��CF=EF����DCF=��DCB=90�㣬
�ڡ�DCF���NEF�У�
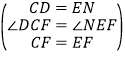 ��
��
���MAD�ա�MEN��
��DF=NF����CFD=��EFN��
�ߡ�EFN+��NFC=90�㣬
���DFC+��CFN=90�㣬
���DFN=90�㣬
��DM��FM��DM=FM
��2��
�⣺���룺DM��FM��DM=FM��
֤�����£���ͼ3������DF��NF������DF��NF��
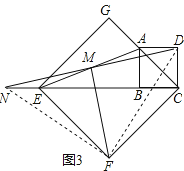
���ı���ABCD�������Σ�
��AD��BC��
�ߵ�E��B��C��ͬһ��ֱ���ϣ�
��AD��CN��
���ADN=��MNE��
�ڡ�MAD���MEN�У�
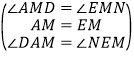 ��
��
���MAD�ա�MEN��
��DM=MN��AD=EN��
��AD=CD��
��CD=NE��
��CF=EF��
�ߡ�DCF=90��+45��=135�㣬��NEF=180�㩁45��=135�㣬
���DCF=��NEF��
�ڡ�DCF���NEF�У�
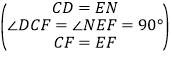 ��
��
���MAD�ա�MEN��
��DF=NF����CFD=��EFN��
�ߡ�CFD+��EFD=90�㣬
���NFE+��EFD=90�㣬
���DFN=90�㣬
��DM��FM��DM=FM��
����������1������DF��NF�����ı���ABCD��CGEF�������Σ��õ�AD��BC��BC��GE�����ǵõ�AD��GE����á�DAM=��NEM��֤�á�MAD�ա�MEN���ó�DM=MN��AD=EN���Ƴ���MAD�ա�MEN��֤����DFN�ǵ���ֱ�������Σ����ɵõ����ۣ�
��2������DF��NF�����ı���ABCD�������Σ��õ�AD��BC���ɵ�E��B��C��ͬһ��ֱ���ϣ����ǵõ�AD��CN����á�DAM=��NEM��֤�á�MAD�ա�MEN���ó�DM=MN��AD=EN���Ƴ���MAD�ա�MEN��֤����DFN�ǵ���ֱ�������Σ����ǽ��۵õ���
�����㾫����������Ҫ������ƽ���ı��ε����ʺ���ͼ-λ�Ʊ任�����֪ʶ�㣬��Ҫ����ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�֣���Ӧ�㵽λ�����ĵľ���Ⱦ���λ�Ʊȣ���Ӧ�߶εıȵ���λ�Ʊȣ�λ�Ʊ�Ҳ��˳����֪ͼ�ε�λ��ͼ������������λ�����ĵ��������һ����λ�����ģ�λ�Ʊ���������Ҫ�ز�����ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������yl=x��x��0���� ![]() ��x��0����ͼ����ͼ��ʾ������ۣ� ��������ͼ��Ľ���A������Ϊ��3��3����
��x��0����ͼ����ͼ��ʾ������ۣ� ��������ͼ��Ľ���A������Ϊ��3��3����
�ڵ�x��3ʱ��y2��y1��
�۵�x=1ʱ��BC=8��
�ܵ�x������ʱ��yl����x�����������y2����x���������С��
������ȷ���۵������ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊa��b���Խ��߳�Ϊc�ij�����ֽƬABCD���Ƶ�C˳ʱ����ת90��õ�������FGCE������AF��ͨ���ò�ͬ������������ABEF���������֤���ɶ���������д����֤�Ĺ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����������ѧ��ѧϰ��ѧ����Ȥ������ѧ���Ĵ��¾��ٰ조��ת��ѧ�����������мס��ҡ�������С������������ί���о����桢С��չʾ�������������Ϊ��С���֣�����ɼ������ٷ��Ƽ�¼���ס��ҡ�������С�����÷������
С�� | �о����� | С��չʾ | ��� |
�� | 91 | 80 | 78 |
�� | 81 | 74 | 85 |
�� | 79 | 83 | 90 |
��1�������С���ƽ���ɼ������Ӹ߷ֵ��ͷ�ȷ��С�������˳��
��2����������о�����ռ40%��С��չʾռ30%�����ռ30%�����С��ijɼ����ĸ�С��ijɼ���ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˱Ƚ��г��ϼס������ֵ�����ÿ����ʱ����������������ֵ������У��������ȡ10̨���в��ԣ����ֵ�������ʱ�����������±�����λ���룩��
��� ���� | һ | �� | �� | �� | �� | �� | �� | �� | �� | ʮ |
���ֵ����� | 1 | ��3 | ��4 | 4 | 2 | ��2 | 2 | ��1 | ��1 | 2 |
���ֵ����� | 4 | ��3 | ��1 | 2 | ��2 | 1 | ��2 | 2 | ��2 | 1 |
(1) ����ס������ֵ�������ʱ����ƽ������
(2) ����ס������ֵ�������ʱ���ķ��
(3) ���ݾ��飬��ʱ�ȶ��ԽϺõĵ������������ţ����������͵ĵ����Ӽ۸���ͬ�����ʣ��������ֵ����ӣ�Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ABC�У���ACB=90�㣬AC=BC����EAC=90�㣬��MΪ����AE������һ�㣨����A�غϣ�������CM�����߶�CM�Ƶ�C��˳ʱ�뷽����ת90��õ��߶�CN��ֱ��NB�ֱ�ֱ��CM������AE�ڵ�F��D��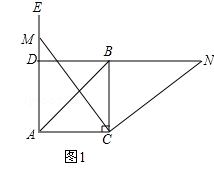
��1��ֱ��д����NDE�Ķ���.
��2����ͼ2��ͼ3������EACΪ��ǻ�۽�ʱ�������������䣬��1���еĽ����Ƿ����仯��������䣬ѡȡ����һ���������֤��������仯����˵������.

��3����ͼ4������EAC=15�㣬��ACM=60�㣬ֱ��CM��AB����G��BD=![]() �������������䣬���߶�AM�ij���
�������������䣬���߶�AM�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD�У���E��F�ֱ��DZ�BC��AB�ϵĵ㣬��CE=BF������DE������E��EG��DE��ʹEG=DE������FG��FC��
��1�����жϣ�FG��CE��������ϵ�� �� λ�ù�ϵ����
��2����ͼ2������E��F�ֱ��DZ�CB��BA�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ�������������жϲ�����֤����
��3����ͼ3������E��F�ֱ��DZ�BC��AB�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ��������ֱ��д������жϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
С����������һ�����⣺��ͼ1����ABC�У�AB=AC����D��BC���ϣ���DAB=��ABD��BE��AD������ΪE����֤��BC=2AE��
С����̽�����֣�����A��AF��BC������ΪF���õ���AFB=��BEA���Ӷ���֤��ABF�ա�BAE����ͼ2����ʹ����õ������
��1�������Ķ����ϻش𣺡�ABF���BAEȫ�ȵ������� AAS���SSS������SAS������ASA������AAS����HL���е�һ����
�ο�С��˼������ķ���������������⣺
��2����ͼ3����ABC�У�AB=AC����BAC=90�㣬DΪBC���е㣬EΪDC���е㣬��F��AC���ӳ����ϣ��ҡ�CDF=��EAC����CF=2����AB�ij���
��3����ͼ4����ABC�У�AB=AC����BAC=120�㣬��D��E�ֱ���AB��AC���ϣ���AD=kDB������0��k�� ![]() ������AED=��BCD����
������AED=��BCD���� ![]() ��ֵ���ú�k��ʽ�ӱ�ʾ����
��ֵ���ú�k��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й�������д��ᡱ�����������̨����������ѧ����ίԱ����������Ľ�Ŀ��ϣ��ͨ����Ŀ�IJ�����������������˹�ע�Ժ����Ļ���ѧϰ��ijУ��չ��һ�Ρ�������д��������ÿλ����ѧ����д40�����֣����������������ȡ����ѧ������д���������д��ȷ�ĺ��ָ���x���Ƴ�����ͼ������������ͳ��ͼ��
����������Ϣ�ش��������⣺
��1�����ι������ȡ����ѧ������д�������д��ȷ�ĺ��ָ���x����Χ��������ࣻ
��2����ȫƵ���ֲ�ֱ��ͼ��
��3��������ͳ��ͼ�У������31��x��41����Ӧ������Բ�ĽǵĴ�С��
��4������У����1200��ѧ���������д��ȷ�ĺ��ָ���������21����Ϊ���ã�������Ƹ�У���Ρ�������д�������ﵽ���õ�ѧ��������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com