
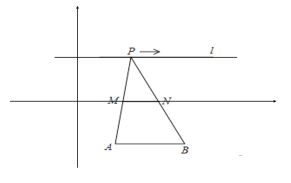
【题目】如图,在直角坐标系中,点![]() ,
,![]() 为定点,A(2,-3),B(4,-3),定直线
为定点,A(2,-3),B(4,-3),定直线![]() ,
,![]() 是
是![]() 上一动点,
上一动点,![]() 到AB的距离为6,
到AB的距离为6,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,对下列各值:①线段
的中点,对下列各值:①线段![]() 的长度始终为1;②
的长度始终为1;②![]() 的周长固定不变;③
的周长固定不变;③![]() 的面积固定不变;④若存在点Q使得四边形APBQ是平行四边形,则Q到
的面积固定不变;④若存在点Q使得四边形APBQ是平行四边形,则Q到![]() 所在的直线的距离必为9;其中说法正确的是__(填序号)
所在的直线的距离必为9;其中说法正确的是__(填序号)
【答案】①③④
【解析】
根据三角形的中位线定理可判断①;
根据![]() 、
、![]() 的长度随点
的长度随点![]() 的移动而变化可判断②;
的移动而变化可判断②;
根据![]() 的长度不变,点
的长度不变,点![]() 到
到![]() 的距离等于
的距离等于![]() 与
与![]() 的距离的一半并结合三角形的面积公式可判断③;
的距离的一半并结合三角形的面积公式可判断③;
根据点Q到MN所在的直线的距离等于Q到AB的距离与AB、MN的距离之和可判断④.
解:∵点![]() ,
,![]() 为定点,AB=2,点
为定点,AB=2,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
∴![]() 是
是![]() 的中位线,∴
的中位线,∴![]() ,故①符合题意;
,故①符合题意;
∵![]() 、
、![]() 的长度随点
的长度随点![]() 的移动而变化,
的移动而变化,
∴![]() 的周长会随点
的周长会随点![]() 的移动而变化,故②不符合题意;
的移动而变化,故②不符合题意;
∵![]() 的长度不变,l∥MN,点
的长度不变,l∥MN,点![]() 到
到![]() 的距离等于
的距离等于![]() 与
与![]() 的距离的一半,
的距离的一半,
∴![]() 的面积不变,故③符合题意;
的面积不变,故③符合题意;
∵l到AB的距离为6,点M到AB的距离为3,则Q到MN所在的直线的距离等于Q到AB的距离与AB、MN的距离之和,即为9,故④符合题意;
综上所述,说法正确的是:①③④.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】“三角形的一个外角等于与它不相邻的两个内角的和”揭示了三角形的一个外角与它的两个内角之间的数量关系,请探索并写出三角形没有公共顶点的两个外角与它的第三个内角之间的关系:_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A(-2,1),B(-4,-2),C(-1,-3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)
(1)A′、B′两点的坐标分别为A′______,B′______;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=10.
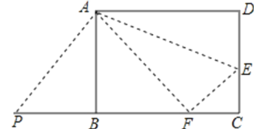
(1)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.求DE的长;
(2)点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长;
(3)M是AD上的动点,在DC上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处,请直接写出线段CT长度的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )
A.![]() B.2020C.2019D.2018
B.2020C.2019D.2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() ,对角线
,对角线![]() 交于点
交于点![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]()
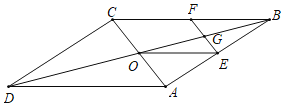
(1)证明:四边形![]() 是平行四边形
是平行四边形
(2)点![]() 是哪些线段的中点,写出结论,并选择一组给出证明.
是哪些线段的中点,写出结论,并选择一组给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
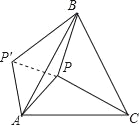
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别骑自行车和摩托车,从同一地点沿相同的路线前往距离80km的某地,图中l1,l2分别表示甲、乙两人离开出发地的距离s(km)与行驶时间t(h)之间的函数关系.请根据图象解答下列问题:
(1)甲、乙两人谁到达目的地较早?早多长时间?
(2)分别求甲、乙两人行驶过程中s与t的函数关系式;
(3)试确定当两辆车都在行驶途中(不包括出发地和目的地)时,t的取值范围;并在这一时间段内,求t为何值时,摩托车行驶在自行车前面?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com