
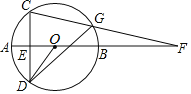
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点G为弧BC上一动点,CG与AB的延长线交于点F,连接OD.
(1)判定∠AOD与∠CGD的大小关系为 ,并求证:GB平分∠DGF.
(2)在G点运动过程中,当GD=GF时,DE=4,BF=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)![]() ,证明见解析;(2)5.
,证明见解析;(2)5.
【解析】
(1)由垂径定理得出![]() ,由圆周角定理即可得出∠AOD=∠CGD;连接BG、BC、BD,由垂径定理得出
,由圆周角定理即可得出∠AOD=∠CGD;连接BG、BC、BD,由垂径定理得出![]() ,由圆周角定理得出∠BCD=∠BGD=∠BDC,由四边形BDCG为圆内接四边形,得出∠BGF=∠BDC,推出∠BGD=∠BGF,即可得出结论;
,由圆周角定理得出∠BCD=∠BGD=∠BDC,由四边形BDCG为圆内接四边形,得出∠BGF=∠BDC,推出∠BGD=∠BGF,即可得出结论;
(2)由SAS证得△BGD≌△BGF,得出BD=BF=4![]() ,由勾股定理得出BE=8,设⊙O的半径为r,则OE=8-r,在Rt△ODE中,根据勾股定理即可求得答案.
,由勾股定理得出BE=8,设⊙O的半径为r,则OE=8-r,在Rt△ODE中,根据勾股定理即可求得答案.
(1)∠AOD=∠CGD;理由如下:
∵AB是⊙O的直径,弦CD⊥AB,
∴![]() ,
,
∴∠AOD=∠CGD,
故答案为:∠AOD=∠CGD;
连接BG、BC、BD,如图所示:

∵AB是⊙O的直径,弦CD⊥AB,
∴![]() ,
,
∴∠BCD=∠BGD=∠BDC,
∵四边形BDCG为圆内接四边形,
∴∠BGF=∠BDC,
∴∠BGD=∠BGF,
∴GB平分∠DGF;
(2)在△BGD和△BGF中, ,
,
∴△BGD≌△BGF(SAS),
∴BD=BF=4![]() ,
,
![]() ,
,
设⊙O的半径为r,则OE=8﹣r,
在Rt△ODE中,![]() ,
,
解得:![]() ,即⊙O的半径为5.
,即⊙O的半径为5.


科目:初中数学 来源: 题型:
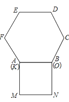
【题目】已知正方形![]() 和正六边形
和正六边形![]() 边长均为1,如图所示,把正方形放置在正六边形外,使
边长均为1,如图所示,把正方形放置在正六边形外,使![]() 边与
边与![]() 边重合,按下列步骤操作:将正方形在正六边形外绕点
边重合,按下列步骤操作:将正方形在正六边形外绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第一次旋转;再绕点
边重合,完成第一次旋转;再绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第二次旋转;此时点
边重合,完成第二次旋转;此时点![]() 经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点
经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点![]() ,
,![]() 之间距离的最大值是______.
之间距离的最大值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
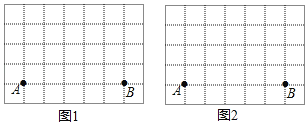
【题目】如图是两张形状,大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A,B均在小正方形的顶点上.
(1)在图1中画出面积为5的△ABC,且△ABC中有一个角为45°;
(2)在图2中画出△ABD,且∠ADB=90°并直接写出△ABD的周长.(C,D都在方格顶点上,每幅图画出一种情况即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
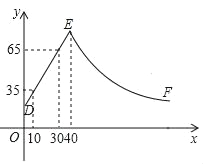
【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=![]() 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=![]() 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax+k(a、k为常数,a≠0),线段AB的两个端点坐标分别为A(﹣1,2),B(2,2).
(1)该二次函数的图象的对称轴是直线 ;
(2)当a=﹣1时,若点B(2,2)恰好在此函数图象上,求此二次函数的关系式;
(3)当a=﹣1时,当此二次函数的图象与线段AB只有一个公共点时,求k的取值范围;
(4)若k=a+3,过点A作x轴的垂线交x轴于点P,过点B作x轴的垂线交x轴于点Q,当﹣1<x<2,此二次函数图象与四边形APQB的边交点个数是大于0的偶数时,直接写出k的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 为边
为边![]() 和
和![]() 上的动点(不含端点),
上的动点(不含端点),![]() .下列三个结论:①当
.下列三个结论:①当![]() 时,则
时,则![]() ;②
;②![]() ;③
;③![]() 的周长不变,其中正确结论的个数是( )
的周长不变,其中正确结论的个数是( )

A.0B.1
C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
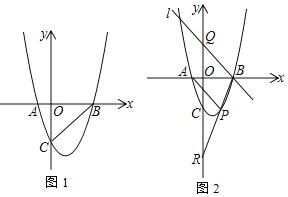
【题目】如图1,在平面直角坐标系中,抛物线y=ax2﹣2x﹣3a与x轴交于A、B两点,与y轴交于C点,OC=OB,点P为抛物线上一动点
(1)求抛物线的解析式;
(2)当点P运动到抛物线对称轴右侧时如图2,连PC、BC、BP得△BCP.设△BCP的面积为s,点P的横坐标为x.若s<![]() ,求x的取值范围;
,求x的取值范围;
(3)当点P运动到第四象限时,连AP、BP,BP交y轴于点R,过B作直线l∥AP交y轴于点Q,问:QR、OC之间是否存在确定的数量关系?若存在,请求出并证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生产某种农产品的成本每千克20元,调查发现,该产品每天销售量y(千克)与销售单价x(元/千克)满足如下关系:![]() ,设这种农产品的销售利润为w元.
,设这种农产品的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)物价部门规定这种产品的销售价不得高于每千克28元,该农户想在这种产品经销季节每天获得150元的利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
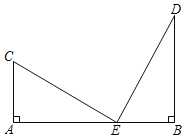
【题目】如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=3,AC=2,AB=m,在线段AB上找一点E,使△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com