
分析 设O是正六边形的中心,AB是正六边形的一边,OC是边心距,则△OAB是正三角形,△OAB的面积的六倍就是正六边形的面积.
解答 解:设O是正六边形的中心,AB是正六边形的一边,OC是边心距,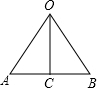
∠AOB=60°,OA=OB=10cm,
则△OAB是正三角形,
∵OC=OA•sin∠A=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$(cm),
∴S△OAB=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×10×5$\sqrt{3}$=25$\sqrt{3}$(cm2),
∴正六边形的面积为25$\sqrt{3}×6$=150$\sqrt{3}$(cm2).
故答案为:150$\sqrt{3}$cm2.
点评 本题考查的正多边形和圆,理解正六边形被半径分成六个全等的等边三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
| 造型 | 甲 | 乙 |
| A | 90 | 30 |
| B | 40 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 路程 | +5 | -3 | +10 | -8 | -6 | +12 | -10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-$\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{a-1}$ | B. | $\frac{a+1}{a-1}$ | C. | $\frac{a}{a+1}$ | D. | a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com