
【题目】某单位需采购一批商品,购买甲商品10件和乙商品15件需资金350元,而购买甲商品15件和乙商品10件需要资金375元.
![]() 求甲、乙商品每件各多少元?
求甲、乙商品每件各多少元?
![]() 本次计划采购甲、乙商品共30件,计划资金不超过460元,
本次计划采购甲、乙商品共30件,计划资金不超过460元,
![]() 最多可采购甲商品多少件?
最多可采购甲商品多少件?
![]() 若要求购买乙商品的数量不超过甲商品数量的
若要求购买乙商品的数量不超过甲商品数量的![]() ,请给出所有购买方案,并求出该单位购买这批商品最少要用多少资金.
,请给出所有购买方案,并求出该单位购买这批商品最少要用多少资金.
【答案】(1)甲商品每件17元,乙商品每件12元;(2)①最多可采购甲商品20件;②购买方案有四种,
方案一:甲商品20件,乙商品10件,此时花费为:20×17+10×12=460(元);
方案二:甲商品19件,乙商品11件,此时花费为:19×17+11×12=455(元);
方案三:甲商品18件,乙商品12件,此时花费为:18×17+12×12=450(元);
方案四:甲商品17件,乙商品13件,此时花费为:17×17+13×12=445(元).
即购买甲商品17件,乙商品13件时花费最少,最少要用445元.
【解析】
(1)根据题意可以列出相应的二元一次方程组,从而可以解答本题;
(2)根据题意可以列出相应的不等式,从而可以解答本题.
解:(1)设甲商品每件x元,乙商品每件y元,
![]() ,
,
解得,![]() ,
,
即甲商品每件17元,乙商品每件12元;
(2)①设采购甲商品m件,
17m+12(30-m)≤460,
解得,m≤20,
即最多可采购甲商品20件;
②由题意可得,
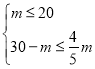 ,
,
解得,![]() ,
,
∴购买方案有四种,
方案一:甲商品20件,乙商品10件,此时花费为:20×17+10×12=460(元),
方案二:甲商品19件,乙商品11件,此时花费为:19×17+11×12=455(元),
方案三:甲商品18件,乙商品12件,此时花费为:18×17+12×12=450(元),
方案四:甲商品17件,乙商品13件,此时花费为:17×17+13×12=445(元).
即购买甲商品17件,乙商品13件时花费最少,最少要用445元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,要建一个面积为140平方米的仓库,仓库的一边靠墙,这堵墙长16米;在与墙平行的一边,要开一扇2米宽的门.已知围建仓库的现有木板材料可使新建板墙的总长为32米,那么这个仓库设计的长和宽应分别为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣![]() x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣
x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣![]() x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣
x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣![]() x+3于点Q,则当PQ=BQ时,a的值是_____.
x+3于点Q,则当PQ=BQ时,a的值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列问题,列出关于![]() 的方程,并将其化为一元二次方程的一般形式
的方程,并将其化为一元二次方程的一般形式
(1)有一个三位数,它的个位数字比十位数字大![]() ,十位数字比百位数字小
,十位数字比百位数字小![]() ,三个数字的平方和的
,三个数字的平方和的![]() 倍比这个三位数小
倍比这个三位数小![]() ,求这个三位数.
,求这个三位数.
(2)如果一个直角三角形的两条直角边长之和为![]() ,面积为
,面积为![]() ,求它的两条直角边的长.
,求它的两条直角边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,点D在边BC上
,点D在边BC上![]() 与B、C不重合
与B、C不重合![]() ,四边形ADEF为正方形,过点F作
,四边形ADEF为正方形,过点F作![]() ,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:![]() ;
;![]() :
:![]() :2;
:2;![]() ;
;![]() ,其中正确的结论的个数是()
,其中正确的结论的个数是()

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边![]() 内一点
内一点![]() 将
将![]() 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() 已知
已知![]()
![]() .
.
![]() 求证:
求证:![]() 是等边三角形;
是等边三角形;
![]() 当
当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 探究:当
探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,它的图象经过点
,它的图象经过点![]() .
.
![]() 若该图象与
若该图象与![]() 轴的一个交点为
轴的一个交点为![]() .
.
①求二次函数![]() 的表达式;
的表达式;
②出该二次函数的大致图象,并借助函数图象,求不等式![]() 的解集;
的解集;
![]() 当
当![]() 取
取![]() ,
,![]() 时,二次函数图象与
时,二次函数图象与![]() 轴正半轴分别交于点
轴正半轴分别交于点![]() ,点
,点![]() .如果点
.如果点![]() 在点
在点![]() 的右边,且点
的右边,且点![]() 和点
和点![]() 都在点
都在点![]() 的右边.试比较
的右边.试比较![]() 和
和![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明骑自行车从家里出发到野外郊游.从家出发1小时后到达南亚所(景点),游玩一段时间后按原速前往湖光岩.小明离家1小时50分钟,妈妈驾车沿相同路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.

(1)求小明骑车的速度和在南亚所游玩的时间;
(2)若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() .一只蝉从点
.一只蝉从点![]() 沿
沿![]() 方向以
方向以![]() 的速度爬行,一只螳螂为了捕捉这只蝉,由点
的速度爬行,一只螳螂为了捕捉这只蝉,由点![]() 沿
沿![]() 方向以
方向以![]() 的速度爬行,一段时间后,它们分别到达了点
的速度爬行,一段时间后,它们分别到达了点![]() ,
,![]() 的位置.若此时
的位置.若此时![]() 的面积为
的面积为![]() ,求它们爬行的时间.
,求它们爬行的时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com