
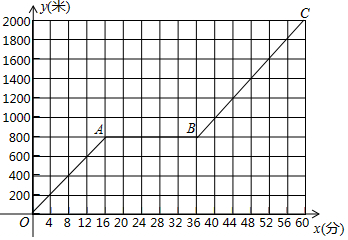
 小明家到公园的路程为2000米,小明爸爸和小明先后从家出发步行去公园.爸爸先出发一直匀速前行,小明在爸爸走出200米后出发,途中他在休闲广场观棋停留一段时间.小明所走路程y(米)与步行时间x(分)的函数图象如图所所示.
小明家到公园的路程为2000米,小明爸爸和小明先后从家出发步行去公园.爸爸先出发一直匀速前行,小明在爸爸走出200米后出发,途中他在休闲广场观棋停留一段时间.小明所走路程y(米)与步行时间x(分)的函数图象如图所所示.分析 (1)利用待定系数法即可解决问题.
(2)根据题意图象经过(0,200),(20,800)画出图象即可.
(3)少观棋8分钟即可比爸爸早8分钟到达公园.
解答 解:(1)设直线BC所对应的函数表达式为y=kx+b,
将(36,800),(60,2000)代入得到$\left\{\begin{array}{l}{36k+b=800}\\{60k+b=2000}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=50}\\{b=-1000}\end{array}\right.$,
∴直线BC所对应的函数表达式为y=50x-1000.
(2)小明的爸爸所走的路程y(米)与小明的步行时间x(分)的函数图象.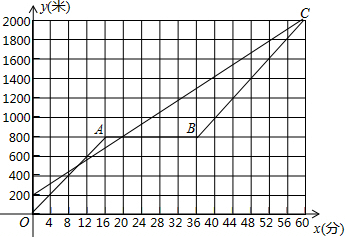
(3)由图象可知,小明与爸爸同时到达目的地,所以少观棋8分钟即可比爸爸早8分钟到达公园.
点评 本题考查一次函数的应用,待定系数法确定函数解析式等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 阅读材料
阅读材料查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m4•m5=m9 | B. | 5x-7x=-2x | ||
| C. | (-x)5÷(-x)2=-x3 | D. | $\frac{{a}^{2}+4a+4}{-{a}^{2}+4}$=$\frac{a+2}{a-2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
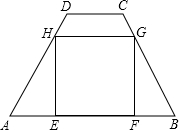 如图,在四边形ABCD中,AB∥CD,AB=15,CD=5,AD=BC=13,矩形EFGH内接于四边形ABCD中.
如图,在四边形ABCD中,AB∥CD,AB=15,CD=5,AD=BC=13,矩形EFGH内接于四边形ABCD中.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
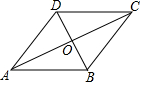 如图,平行四边形ABCD的对角线AC,BD相交于点O,补充下面一个条件,不能判定平行四边形ABCD是菱形的是( )
如图,平行四边形ABCD的对角线AC,BD相交于点O,补充下面一个条件,不能判定平行四边形ABCD是菱形的是( )| A. | AB=BC | B. | AO=BO | C. | ∠DOC=90° | D. | ∠CDO=∠ADO |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
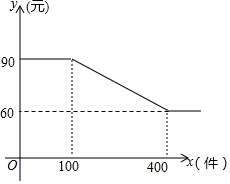 某衬衫厂生产某品牌衬衫的成本价为50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍.
某衬衫厂生产某品牌衬衫的成本价为50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com