
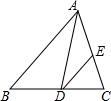
 如图,已知AD是△ABC的角平分线,过点D作DE∥AB,交AC于点E,∠B=50°,∠ADE=30°,求∠C的度数.
如图,已知AD是△ABC的角平分线,过点D作DE∥AB,交AC于点E,∠B=50°,∠ADE=30°,求∠C的度数.  鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,?ABCD中,AD=10,AB=8,P为BC上的任意一点,E,F,G,H分别为AB,AP,DP,DC的中点,则EF+GH的长是( )
如图,?ABCD中,AD=10,AB=8,P为BC上的任意一点,E,F,G,H分别为AB,AP,DP,DC的中点,则EF+GH的长是( )| A. | 10 | B. | 8 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | |
| 进价(元/件) | 40 | 60 |
| 售价(元/件) | 60 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知如图所示,矩形ABCD,P为BC上的一点,连接AP,过D点做DH⊥AP交AP与H,AB=2$\sqrt{2}$,BC=4,当△CDH为等腰三角形时,则BP=4-2$\sqrt{2}$、2$\sqrt{2}$或2.
已知如图所示,矩形ABCD,P为BC上的一点,连接AP,过D点做DH⊥AP交AP与H,AB=2$\sqrt{2}$,BC=4,当△CDH为等腰三角形时,则BP=4-2$\sqrt{2}$、2$\sqrt{2}$或2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC的中线AD、BE、CF相交于点G,H、I分别是BG、CG的中点.
如图,△ABC的中线AD、BE、CF相交于点G,H、I分别是BG、CG的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平行于直线y=x的直线l不经过第四象限,且与函数$y=\frac{3}{x}$(x>0)的图象交于点A,过A作AB⊥y轴于点B,AC⊥x轴于点C,四边形ABOC的周长为8.
平行于直线y=x的直线l不经过第四象限,且与函数$y=\frac{3}{x}$(x>0)的图象交于点A,过A作AB⊥y轴于点B,AC⊥x轴于点C,四边形ABOC的周长为8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | -3 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com