
【题目】某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为x(0<x<0.5).
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ① |
平均步长(米/步) | 0.6 | ② |
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形网格MNPQ中,每个小方格的边长都相等,正方形ABCD的顶点在正方形MNPQ的4条边的小方格顶点上.

(1)设正方形MNPQ网格内的每个小方格的边长为1,求:
①△ABQ,△BCM,△CDN,△ADP的面积;
②正方形ABCD的面积.
(2)设MB=a,BQ=b,利用这个图形中的直角三角形和正方形的面积关系,你能验证已学过的哪一个数学公式或定理吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是4,点E是BC的中点,连接DE,DF⊥DE交BA的延长线于点F.连接EF、AC,DE、EF分别与C交于点P、Q,则PQ=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B. 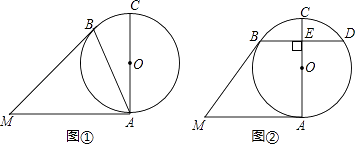
(1)如图①,若∠BAC=23°,求∠AMB的大小;
(2)如图②,过点B作BD∥MA,交AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与思考:一张边长为a的正方形桌面,因为实际需要,需将正方形边长增加b,从而得到一个更大的正方形,木工师傅设计了如图所示的方案:
(1)方案中大正方形的边长都是 ,所以面积为 ;
(2)小明还发现:方案中大正方形的面积还可以用四块小四边形的面积和来表示 ;
(3)你有什么发现,请用数学式子表达 ;
(4)利用(3)的结论计算20.182+2×20.18×19.82+19.822的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE.
(1)若CB=4,BE=5,求AE的长;
(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC;
小洁在遇到此问题时不知道怎么下手,秦老师提示他可以过点C作CH![]() CF,交DB于点H,先证明△AFC
CF,交DB于点H,先证明△AFC![]() △BHC,然后继续思考,并鼓励小洁把证明过程写出来.请你帮助小洁完成这个问题的证明过程.
△BHC,然后继续思考,并鼓励小洁把证明过程写出来.请你帮助小洁完成这个问题的证明过程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com