
分析 (1)根据“首同尾补”的运算规律解答即可;
(2)先利用实例计算得到运算规律,再根据“首同尾补”的说理方法验证;
(3)根据题意即可得到结论.
解答 解:(1)63×67=4221,91×99=9009;
故答案为:4221,9009;
(2)“首补尾同”:
设十位数字为a,个位数字为b,互补的十位数字为c,
(10a+b)(10c+b)=100(a•c+b)+b2;
(3)已知两数的十位数字为a,个位数字分别为b,c且b,c“互补”,即b+c=10,
求证:这两数的积(10a+b)(10a+c)=100a(a+1)+bc,
证明:(10a+b)(10a+c)=100a2+10bc+10ac+bc=100a2+10a(b+c)+bc=100a2+10a×10+bc=100a2+100a+bc=100a(a+1)+bc.
点评 本题是对数字变化规律的考查,读懂题目信息,理解“首同尾补”的数字的变化规律的探讨过程是解题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
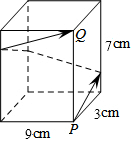 如图,长方体的底面边长分别为9cm和3cm,高为7cm,若一只蚂蚁从P开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为25cm.
如图,长方体的底面边长分别为9cm和3cm,高为7cm,若一只蚂蚁从P开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为25cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com