
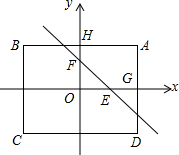
 如图,已知矩形ABCD的面积为48,以此矩形的对称轴为坐标轴建立直角坐标系.设A(x,y),其中x>0,y>0.
如图,已知矩形ABCD的面积为48,以此矩形的对称轴为坐标轴建立直角坐标系.设A(x,y),其中x>0,y>0.分析 (1)由点A的坐标结合矩形ABCD的面积为48,即可得出4xy=48,将其变形后即可得出结论;
(2)假设存在,由一次函数的解析式可得出点E、F的坐标,通过分割图形求面积法结合△AFE的面积是矩形ABCD面积的$\frac{1}{8}$,即可得出关于m的方程,解方程即可得出结论.
解答 解:(1)∵矩形ABCD的面积为48,A(x,y),
∴4xy=48,
∴y=$\frac{12}{x}$(x>0).
(2)假设存在.
当x=0时,y=2,
∴F(0,2);
当y=0时,有0=mx+2,
解得:x=-$\frac{2}{m}$,
∴E(-$\frac{2}{m}$,0).
∴S△AEF=S矩形AHOG-S△AHF-S△OEF-S△AEG=3×4-$\frac{1}{2}$×(3-2)×4-$\frac{1}{2}$×2×(-$\frac{2}{m}$)-$\frac{1}{2}$×3×(4+$\frac{2}{m}$)=$\frac{1}{8}$×48,
即4-$\frac{1}{m}$=6,
解得:m=-$\frac{1}{2}$,
经检验m=-$\frac{1}{2}$是分式方程4-$\frac{1}{m}$=6的解.
故存在实数m=-$\frac{1}{2}$,使得△AFE的面积是矩形ABCD面积的$\frac{1}{8}$.
点评 本题考查了一次函数图象上点的坐标特征、矩形的性质以及三角形的面积,解题的关键是:(1)根据矩形的面积为48找出x、y之间的关系;(2)找出关于m的方程.本题属于中档题,难度不大,解决该题型题目时,利用分割图形法求出三角形的面积是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将3枚相同的硬币放入一个3×4的长方形格子中(每个小正方形格子只能放1枚硬币).则所放的3枚硬币中,任意两枚都不同行且不同列的概率为$\frac{6}{55}$.
如图,将3枚相同的硬币放入一个3×4的长方形格子中(每个小正方形格子只能放1枚硬币).则所放的3枚硬币中,任意两枚都不同行且不同列的概率为$\frac{6}{55}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com