
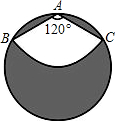
 如图所示,有一个直径是1m的圆形铁皮,要从中剪出一个半径为$\frac{1}{2}$且圆心角是120°的扇形ABC.求被剪掉后剩余阴影部分的面积.
如图所示,有一个直径是1m的圆形铁皮,要从中剪出一个半径为$\frac{1}{2}$且圆心角是120°的扇形ABC.求被剪掉后剩余阴影部分的面积. 分析 设O为圆心,连接OA,OB,OC,BC,由OA=OC=OB,且AB=AC,从而得出三角形ABO与三角形ACO全等,可得AB=AC=0.5m,先求得圆的面积,再求得扇形的面积,求差即可.
解答 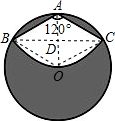 解:(1)设O为圆心,连接OA、OB,OC,BC,且OA与BC交于点D,如图所示:
解:(1)设O为圆心,连接OA、OB,OC,BC,且OA与BC交于点D,如图所示:
在△ABO和△ACO中,
$\left\{\begin{array}{l}{OB=OC}\\{AB=AC}\\{OA=OA}\end{array}\right.$,
∴△ABO≌△ACO (SSS),
又∵∠BAC=120°,
∴∠BAO=∠CAO=60°,又OA=OB,
∴△ABO是等边三角形,
∴AB=OA=$\frac{1}{2}$×1=$\frac{1}{2}$(米),
∴S扇形ABC=$\frac{120π×(\frac{1}{2})^{2}}{360}$=$\frac{π}{12}$m2,
∴S阴影=π ($\frac{1}{2}$)2-$\frac{π}{12}$=$\frac{π}{6}$m2.
点评 本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:选择题
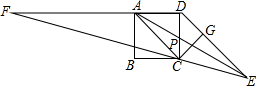 如图,四边形ABCD是正方形,DE∥AC,CE=AC,EC的延长线DA的延长线交于F,连AE交CD于P,作CG⊥DE于G,则下列结论:①AE平分∠CED;②S△ADP=S△EPC;③∠F=∠EAC;④CE=2CG.其中正确的说法有( )
如图,四边形ABCD是正方形,DE∥AC,CE=AC,EC的延长线DA的延长线交于F,连AE交CD于P,作CG⊥DE于G,则下列结论:①AE平分∠CED;②S△ADP=S△EPC;③∠F=∠EAC;④CE=2CG.其中正确的说法有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y3<y1<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com