
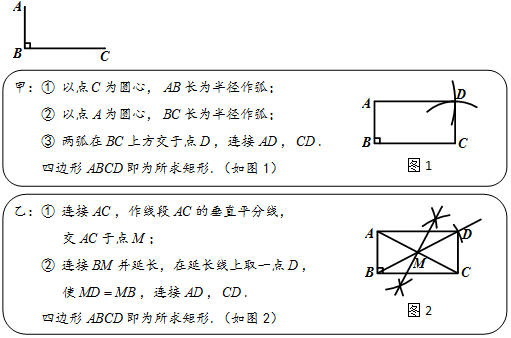
分析 对于甲同学:利用作法得到CD=AB,AD=BC,则根据平行四边形的判定方法得到四边形ABCD为平行四边形,然后判定四边形ABCD为矩形;对于乙同学:利用作法得到AM=CM,BM=DM,则根据平行四边形的判定方法得到四边形ABCD为平行四边形,然后判定四边形ABCD为矩形.
解答 解:甲的作图依据是:两组对边分别相等的四边形是平行四边形;有一个角是直角的平行四边形是矩形;
乙的作图依据是:对角线互相平分的四边形是平行四边形;有一个角是直角的平行四边形是矩形.
故答案为两组对边分别相等的四边形是平行四边形;有一个角是直角的平行四边形是矩形;对角线互相平分的四边形是平行四边形;有一个角是直角的平行四边形是矩形.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了矩形的判定方法.


科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,连接AE交CD于点F.
如图,在?ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,连接AE交CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
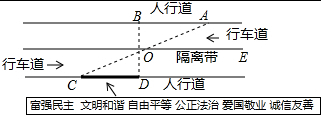 小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )
小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )| A. | ∠BOA=∠DOC | B. | AB∥CD | ||
| C. | ∠ABD=90° | D. | 与∠AOE相等的角共有2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (27a8)÷[($\frac{1}{3}{a}^{3}$)÷(9a2)] | B. | [(27a8)÷($\frac{1}{3}{a}^{3}$)]÷(9a2) | C. | (27$÷\frac{1}{3}÷9$)a8-3-2 | D. | [(27a3)÷(9a2)]÷($\frac{1}{3}{a}^{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com