
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -$\frac{3}{16}$ | -4 | -$\frac{5}{2}$ | -2 | -$\frac{5}{2}$ | … |
分析 (1)利用表中数据和抛物线的对称性可得到抛物线的对称轴为直线x=1,于是可判断x=3和x=-1时的函数值相等;
(2)利用表中数据得到抛物线的顶点坐标为(1,-2),则可设顶点y=a(x-1)2-2,然后把一组对应值代入求出a即可.
解答 解:(1)∵x=0和x=2时的函数值都为-$\frac{5}{2}$,
∴抛物线的对称轴为直线x=1,
∴x=3和x=-1时的函数值相等,
即二次函数当x=3时,y的值为-4;
(2)抛物线的顶点坐标为(1,-2),
设抛物线解析式为y=a(x-1)2-2,
把(-1,-4)代入得a(-1-1)2-2=-4,解得a=-$\frac{1}{2}$,
故抛物线解析式为y=-$\frac{1}{2}$(x-1)2-2.
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解,


科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{a-b}$ | B. | $\frac{b}{a-b}$ | ||
| C. | $\frac{{a}^{2}+ab+2{b}^{2}}{{a}^{2}-{b}^{2}}$ | D. | $\frac{{a}^{2}+ab+{b}^{2}}{{a}^{2}-{b}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
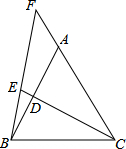 如图,△ABC为等边三角形,D为AB上一点,点E为CD延长线上一点,CE=CB,连接BE并延长交CA的延长线于点F,若AD=3,CF=7,则CD=4.
如图,△ABC为等边三角形,D为AB上一点,点E为CD延长线上一点,CE=CB,连接BE并延长交CA的延长线于点F,若AD=3,CF=7,则CD=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 数学课上,老师要求同学们画函数y=|x|的图象,小红联想绝对值的性质得y=x(x≥0)或y=-x(x≤0),于是她很快作出了该函数的图象(如图),和你的同桌交流一下,小红的作法对吗?如果不对,试画出该函数的图象.
数学课上,老师要求同学们画函数y=|x|的图象,小红联想绝对值的性质得y=x(x≥0)或y=-x(x≤0),于是她很快作出了该函数的图象(如图),和你的同桌交流一下,小红的作法对吗?如果不对,试画出该函数的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
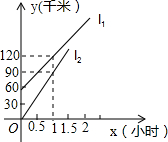 已知A,B地相距225千米,甲,乙两车都从A地出发,沿同一条高速公路前往B地,甲比乙早出发1小时,如图所示的l1,l2分别表示甲乙两车相对于出发地A的距离y(千米)与乙车行驶时间x(小时)之间的关系.根据图象提供的信息,解答下列问题:
已知A,B地相距225千米,甲,乙两车都从A地出发,沿同一条高速公路前往B地,甲比乙早出发1小时,如图所示的l1,l2分别表示甲乙两车相对于出发地A的距离y(千米)与乙车行驶时间x(小时)之间的关系.根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com