
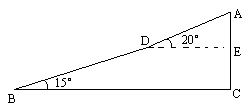
如图,一勘测人员从B点出发,沿坡角为![]() 的坡面以5千米/时的速度行至D处,用了12分钟,然后沿坡角为
的坡面以5千米/时的速度行至D处,用了12分钟,然后沿坡角为![]() 的坡面以3千米/时的速度到达山顶A点处,用了10分钟.求山高(即AC的长度)及A,B两点间的水平距离(即BC的长)(精确到0.01千米).
的坡面以3千米/时的速度到达山顶A点处,用了10分钟.求山高(即AC的长度)及A,B两点间的水平距离(即BC的长)(精确到0.01千米).
科目:初中数学 来源: 题型:
 如图,一勘测人员从山脚B点出发,沿坡度为1:3的坡面BD行至D点处时,他的垂直高度上升了15米;然后再从D点处沿坡角为45°的坡面DA以20米/分钟的速度到达山顶A点时,用了10分钟.
如图,一勘测人员从山脚B点出发,沿坡度为1:3的坡面BD行至D点处时,他的垂直高度上升了15米;然后再从D点处沿坡角为45°的坡面DA以20米/分钟的速度到达山顶A点时,用了10分钟.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一勘测人员从B点出发,沿坡角为15°的坡面以5千米/时的速度行至D点,用了12分钟,然后沿坡角为20°的坡面以3千米/时的速度到达山顶A点,用了10分钟.求山高(即AC的长度)及A、B两点的水平距离(即BC的长度)(精确到0.01千米).(sin15°=0.2588,cos15°=0.9659,sin20°=0.3420,cos20°=0.9397)
如图,一勘测人员从B点出发,沿坡角为15°的坡面以5千米/时的速度行至D点,用了12分钟,然后沿坡角为20°的坡面以3千米/时的速度到达山顶A点,用了10分钟.求山高(即AC的长度)及A、B两点的水平距离(即BC的长度)(精确到0.01千米).(sin15°=0.2588,cos15°=0.9659,sin20°=0.3420,cos20°=0.9397)查看答案和解析>>
科目:初中数学 来源: 题型:
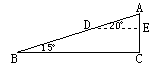
 如图,一勘测人员从B点出发,沿坡角为15°的坡面以5千米/时的速度行至D处,用了12分钟,然后沿坡角为20°的坡面以3千米/时的速度到达山顶A点处,用了10分钟,求山高(即AC的长度)及(即BC的长)(精确到0.01千米).
如图,一勘测人员从B点出发,沿坡角为15°的坡面以5千米/时的速度行至D处,用了12分钟,然后沿坡角为20°的坡面以3千米/时的速度到达山顶A点处,用了10分钟,求山高(即AC的长度)及(即BC的长)(精确到0.01千米).查看答案和解析>>
科目:初中数学 来源:2012年北师大版初中数学九年级下1.3三角函数的有关计算练习卷(解析版) 题型:解答题
如图,一勘测人员从B点出发,沿坡角为15°的坡面以5千米/时的速度行至D处,用了12分钟,然后沿坡角为20°的坡面以3千米/时的速度到达山顶A点处,用了10 分钟,求山高(即AC的长度)及A、B两点间的水平距离(即BC的长)(精确到0.01千米).
查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com