
分析 令绝对值中式子为0,求出x的值,分类讨论x的范围,原式利用绝对值的代数意义化简,计算即可得到a的最小值.
解答 解:令x+1=0,x-2=0,x-2014=0,得到x=-1,2,2014,
当x≤-1时,原式=-x-1+2-x+2014-x=-3x+2015,最小值为2018;
当-1<x≤2时,原式=x+1+2-x+2014-x=-x+2017,最小值为2015;
当2≤x≤2014时,原式=x+1+x-2+2014-x=2013+x,最小值为2015;
当x≥2014时,原式=x+1+x-2+x-2014=3x-2015,最小值为4027,
综上,当x=2时,a有最小值为2015,
故答案为:2;2015
点评 此题考查了绝对值,熟练掌握绝对值的代数意义是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
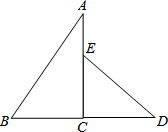 如图,是一副三角板组成的图形.
如图,是一副三角板组成的图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
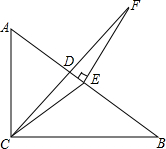 如图,在△ABC中,∠ACB=90°,CD是角平分线,点E在AB上,∠ECB=∠B,EF⊥AB交CD的延长线于点F,求证:∠F=∠DCE.
如图,在△ABC中,∠ACB=90°,CD是角平分线,点E在AB上,∠ECB=∠B,EF⊥AB交CD的延长线于点F,求证:∠F=∠DCE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 己知E为△ABC内部一点,AE延长线交边BC于点D,连按BE、CE,∠BED=∠BAC=2∠DEC.
己知E为△ABC内部一点,AE延长线交边BC于点D,连按BE、CE,∠BED=∠BAC=2∠DEC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.5 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com