
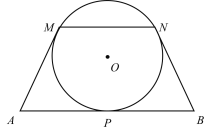
【题目】如图,AB,AM,BN 分别是⊙O 的切线,切点分别为 P,M,N.若 MN∥AB,∠A=60°,AB=6,则⊙O 的半径是( )
A.![]() B.3C.
B.3C.![]()
![]() D.
D.![]()
【答案】D
【解析】
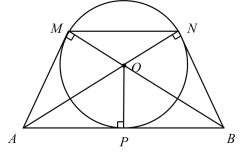
根据题意可判断四边形ABNM为梯形,再由切线的性质可推出∠ABN=60°,从而判定△APO≌△BPO,可得AP=BP=3,在直角△APO中,利用三角函数可解出半径的值.
解:连接OP,OM,OA,OB,ON
∵AB,AM,BN 分别和⊙O 相切,
∴∠AMO=90°,∠APO=90°,
∵MN∥AB,∠A=60°,
∴∠AMN=120°,∠OAB=30°,
∴∠OMN=∠ONM=30°,
∵∠BNO=90°,
∴∠ABN=60°,
∴∠ABO=30°,
在△APO和△BPO中,
 ,
,
△APO≌△BPO(AAS),
∴AP=![]() AB=3,
AB=3,
∴tan∠OAP=tan30°=![]() =
=![]() ,
,
∴OP=![]() ,即半径为
,即半径为![]() .
.
故选D.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标有的三个数值为﹣7,﹣1,3.乙袋中的三张卡片所标的数值为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出卡片上的数值,把x、y分别作为点A的横坐标和纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况.
(2)求点A落在第三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
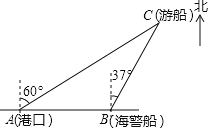
【题目】一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,
(1)求点C到直线AB的距离;
(2)求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
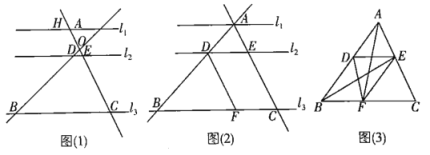
【题目】如图(1),![]() ,直线AB和CH交于点O,分别交
,直线AB和CH交于点O,分别交![]() 于D、E两点,已知
于D、E两点,已知![]() ,
,![]() ,
,![]() .
.
(1)尝试探究:在图(1)中,求DB和AD的长;
(2)类比延伸:平移AB使得A与H重合,如图(2)所示,过点D作![]() ,若
,若![]() ,求线段BF的长;
,求线段BF的长;
(3)拓展迁移:如图(3),若![]() 的面积是10,点D、E分别位于AB、CA上,
的面积是10,点D、E分别位于AB、CA上,![]() ,点F在BC上且
,点F在BC上且![]() ,
,![]() ,如果
,如果![]() 的面积和四边形FCED的面积相等,求这个相等的面积.
的面积和四边形FCED的面积相等,求这个相等的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实视力保护工作,某校组织七年级学生开展了视力保健活动.活动前随机测查了30名学生的视力,活动后再次测查这部分学生的视力.两次相关数据记录如下:
活动前被测查学生视力数据:
![]()
活动后被测查学生视力数据:
![]()
活动后被测查学生视力频数分布表
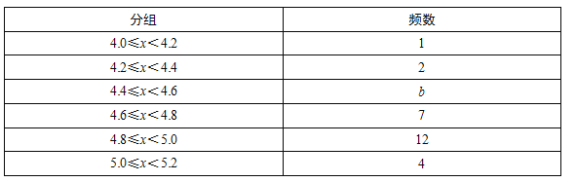
根据以上信息回答下列问题:
(1)填空:a= ,b= ,活动前被测查学生视力样本数据的中位数是 ,活动后被测查学生视力样本数据的众数是 ;
(2)若视力在4.8及以上为达标,估计七年级600名学生活动后视力达标的人数有多少?
(3)分析活动前后相关数据,从一个方面评价学校开展视力保健活动的效果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小尧用“描点法”画二次函数![]() 的 图像,列表如下:
的 图像,列表如下:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
y | … | 5 | 0 | -3 | -4 | -3 | 0 | -5 | … |
(1)由于粗心,小尧算错了其中的一个 y值,请你指出这个算错的y值所对应的 x = ;
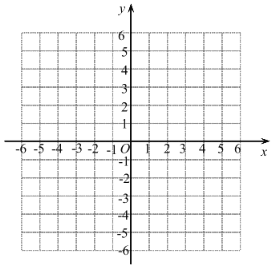
(2)在图中画出这个二次函数![]() 的图像;
的图像;
(3)当 y≥5 时,x 的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是一张等腰直角三角形板,
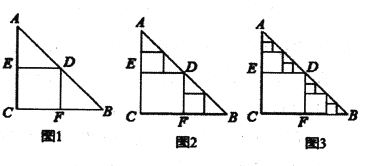
是一张等腰直角三角形板,![]() ,要在这张纸板中剪取正方形(剪法如图1所示),图1中剪法称为第
,要在这张纸板中剪取正方形(剪法如图1所示),图1中剪法称为第![]() 次剪取,记所得的正方形面积为
次剪取,记所得的正方形面积为![]() ;按照图1中的剪法,在余下的
;按照图1中的剪法,在余下的![]() 和
和![]() 中,分别剪取两个全等正方形,称为第
中,分别剪取两个全等正方形,称为第![]() 次剪取,并记这两个正方形面积和为
次剪取,并记这两个正方形面积和为![]() ,(如图2) ;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第
,(如图2) ;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第![]() 次剪取,并记这四个正方形的面积和为
次剪取,并记这四个正方形的面积和为![]() ,(如图3);继续操作下去···则第
,(如图3);继续操作下去···则第![]() 次剪取后,
次剪取后,![]() ___________.
___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”译文:已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?(1丈=10尺,1尺=10寸)设长方形门的宽![]() 尺,可列方程为_______.
尺,可列方程为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的任意两点M![]() ,N
,N![]() ,给出如下定义:点M与点N的“折线距离”为:
,给出如下定义:点M与点N的“折线距离”为:![]()
![]()
![]() .
.

例如:若点M(-1,1),点N(2,-2),则点M与点N的“折线距离”为:![]() .根据以上定义,解决下列问题:
.根据以上定义,解决下列问题:
(1)已知点P(3,-2).
①若点A(-2,-1),则d(P,A)= ;
②若点B(b,2),且d(P,B)=5,则b= ;
③已知点C(m,n)是直线![]() 上的一个动点,且d(P,C)<3,求m的取值范围.
上的一个动点,且d(P,C)<3,求m的取值范围.
(2)⊙F的半径为1,圆心F的坐标为(0,t),若⊙F上存在点E,使d(E,O)=2,直接写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com