
分析 (1)原式先计算乘方运算,再计算乘除运算即可得到结果;
(2)原式逆用乘法分配律计算即可得到结果;
(3)原式先计算乘方运算,再计算乘除运算,即可得到结果;
(4)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(5)原式去括号合并即可得到结果;
(6)原式去括号合并即可得到结果.
解答 解:(1)原式=-64×$\frac{1}{4}$×$\frac{1}{5}$=-$\frac{16}{5}$;
(2)原式=0.75×(-1.53+0.53-3.4)=$\frac{3}{4}$×(-4.4)=-3.3;
(3)原式=-$\frac{1}{2}$×3×18=-27;
(4)原式=-125×(-$\frac{3}{5}$)+32×$\frac{1}{4}$×$\frac{5}{4}$=75+10=85;
(5)原式=8a2b-5ab2-6a2b+8ab2=2a2b+3ab2;
(6)原式=2a2-2ab-8a2+12ab=-6a2+10ab.
点评 此题考查了整式的加减,以及有理数的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:选择题
 如图,将矩形纸带ABCD,沿EF折叠后,C、D两点分别落在C′、D′的位置,经测量得∠EFB=65°,则∠AED′的度数是( )
如图,将矩形纸带ABCD,沿EF折叠后,C、D两点分别落在C′、D′的位置,经测量得∠EFB=65°,则∠AED′的度数是( )| A. | 65° | B. | 55° | C. | 50° | D. | 25° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
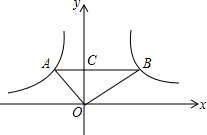 如图,在直角坐标系中,O为坐标原点,函数y1=$\frac{{k}_{1}}{x}$(x<0)和y2=$\frac{{k}_{2}}{x}$(x>0)的图象上,分别有A、B两点,若AB∥x轴且交y轴于点C,且OA⊥OB,S△AOC=$\frac{1}{2}$,S△BOC=$\frac{9}{2}$,则线段AB的长度为( )
如图,在直角坐标系中,O为坐标原点,函数y1=$\frac{{k}_{1}}{x}$(x<0)和y2=$\frac{{k}_{2}}{x}$(x>0)的图象上,分别有A、B两点,若AB∥x轴且交y轴于点C,且OA⊥OB,S△AOC=$\frac{1}{2}$,S△BOC=$\frac{9}{2}$,则线段AB的长度为( )| A. | 3$\sqrt{3}$ | B. | $\frac{10}{3}$$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y1>y3>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com