
【题目】如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2…An﹣1为OA的n等分点,点B1,B2…Bn﹣1为CB的n等分点,连结A1B1,A2B2,…An﹣1Bn﹣1,分别交曲线![]() (x>0)于点C1,C2,…,Cn﹣1.若C15B15=16C15A15,则n的值为_______.(n为正整数)
(x>0)于点C1,C2,…,Cn﹣1.若C15B15=16C15A15,则n的值为_______.(n为正整数)

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
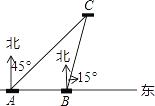
【题目】如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236.
≈2.236.
查看答案和解析>>
科目:初中数学 来源: 题型:
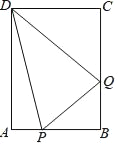
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6cm,BC=8cm,点P从点A沿边AB以1cm/s的速度向点B移动,同时点Q从点B沿边BC以2cm/s的速度向点C移动,当P、Q两点中有一个点到终点时,则另一个点也停止运动.当△DPQ的面积比△PBQ的面积大19.5cm2时,求点P运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
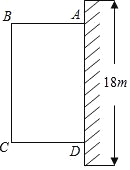
【题目】为了改善小区环境,某小区决定要在一块边靠墙(墙长18m)的空地,修建一个矩形绿地ABCD,绿地一边靠墙,另三边用总长为40m的栅栏围住(如图),设AB边为xm,绿地面积为ym2.
(1)求y与x之间的函数关系,并求出自变量x的取值范围;
(2)绿地的面积能不能为200m2?如果能,求出x的值,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)求出线段AB,曲线CD的解析式,并写出自变量的取值范围;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划按文学、艺术、科普和其他四个类别购买课外读物 9000 册,请根据样本数据,估计学校购买其他类读物 册比较合理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于![]() BG.则其中正确的是( )
BG.则其中正确的是( )
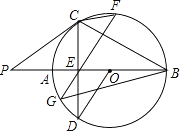
A. ①②④ B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com