
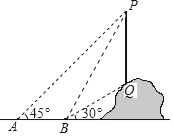
【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,则该电线杆PQ的高度( )
A. 6+2![]() B. 6+
B. 6+![]() C. 10﹣
C. 10﹣![]() D. 8+
D. 8+![]()
【答案】A
【解析】
延长PQ交直线AB于点E,设PE=xm,在Rt△APE和Rt△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE-BE即可列出方程求得x的值,然后在Rt△BQE中利用三角函数求得QE的长,则PQ的长度即可求解.
解:延长PQ交直线AB于点E,设PE=xm.
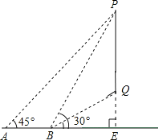
在Rt△APE中,∠A=45°,
则AE=PE=xm,
∵∠PBE=60°,
∴∠BPE=30°,
在Rt△BPE中,
BE=![]() PE=
PE=![]() xm,
xm,
∵AB=AEBE=6m,
则x![]() x=6,
x=6,
解得:x=9+3![]() ,
,
∴BE=3![]() +3 (m),
+3 (m),
在Rt△BEQ中,
QE=![]() BE=
BE=![]() (3
(3![]() +3)= 3+
+3)= 3+![]() (m),
(m),
∴PQ=PEQE=9+3![]() (3+
(3+![]() )=6+2
)=6+2![]() (m).
(m).
故选A.


科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系中,抛物线
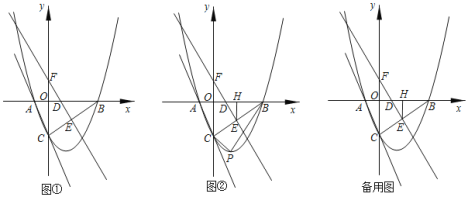
,在平面直角坐标系中,抛物线![]() 分别与x轴交于A,B两点,与y轴交于C点,直线EF垂直平分线段BC,分别交BC于点E,y轴于点F,交x轴于D.
分别与x轴交于A,B两点,与y轴交于C点,直线EF垂直平分线段BC,分别交BC于点E,y轴于点F,交x轴于D.
![]() 判定
判定![]() 的形状;
的形状;
![]() 在线段BC下方的抛物线上有一点P,当
在线段BC下方的抛物线上有一点P,当![]() 面积最大时,求点P的坐标及
面积最大时,求点P的坐标及![]() 面积的最大值;
面积的最大值;
![]() 如图
如图![]() ,过点E作
,过点E作![]() 轴于点H,将
轴于点H,将![]() 绕点E逆时针旋转一个角度
绕点E逆时针旋转一个角度![]() ,
,![]() 的两边分别交线段BO,CO于点T,点K,当
的两边分别交线段BO,CO于点T,点K,当![]() 为等腰三角形时,求此时KT的值.
为等腰三角形时,求此时KT的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
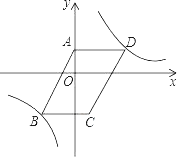
【题目】如图,在平面直角坐标系xOy中,双曲线y=![]() 过ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,SABCD=6.
过ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,SABCD=6.
(1)填空:点A的坐标为 ;
(2)求双曲线和AB所在直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是![]() 的直径,点C、D在
的直径,点C、D在![]() 上,且AD平分
上,且AD平分![]() ,过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F,G为AB的下半圆弧的中点,DG交AB于H,连接DB、GB.
,过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F,G为AB的下半圆弧的中点,DG交AB于H,连接DB、GB.
![]() 证明EF是
证明EF是![]() 的切线;
的切线;
![]() 求证:
求证:![]() ;
;
![]() 已知圆的半径
已知圆的半径![]() ,
,![]() ,求GH的长.
,求GH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为正
为正![]() 的
的![]() 边上一点(
边上一点(![]() 不与点
不与点![]() 重合),点
重合),点![]() 分别在边
分别在边![]() 上,且
上,且![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() (用含
(用含![]() 的式子表示);
的式子表示);
(3)如图2,若点![]() 为
为![]() 边的中点,求证:
边的中点,求证: ![]() .
.
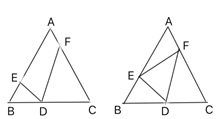
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com