练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

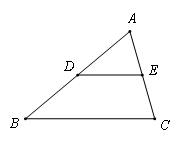
    ⑴证明三角形中位线定理：三角形的中位线平行于第三边，且等于第三边的一半；

    要求：根据图1写出定理的已知、求证、证明；在证明过程中，至少有两外写出推理的依据（“已知”除外）

    ⑵如图2，在□ABCD中，对角线交点为O，A1、B1、C1、D1分别是OA、OB、OC、OD的中点，A2、B2、C2、D2分别是OA1、OB1、OC1、OD1的中点，…以此类推

    若在□ABCD的周长为1，直接用算式表示各四边形的周长之和l；

    ⑶借助图形3反映的规律，猜猜l可能是多少？



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


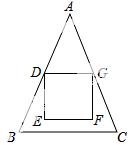
    如图，△ABC中，AB=AC=18，BC=12，正方形DEFG的顶点E，F在△ABC内，顶点D，G分别在AB，AC上，AD=AG，DG=6，则点F到BC的距离为【    】

    A. 1        B. 2         C. 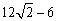         D.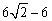

    查看答案和解析>>

    科目：初中数学 来源： 题型：


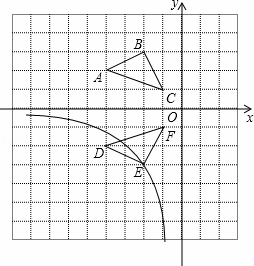
    如图，在边为的1正方形组成的网格中，建立平面直角坐标系，若A（﹣4，2）、B（﹣2，3）、C（﹣1，1），将△ABC沿着x轴翻折后，得到△DEF，点B的对称点是点E，求过点E的反比例函数解析式，并写出第三象限内该反比例函数图象所经过的所有格点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：__________；

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知⊙O的直径为10cm，弦AB=8cm，P是弦AB上的一个动，求OP的长度范围；

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     如图，桌面上有一个一次性纸杯，它的正视图应是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    关于x的方程m（x+h）2+k=0（m，h，k均为常数，m≠0）的解是x1=﹣3，x2=2，则方程m（x+h﹣3）2+k=0的解是（　　）

    　 A． x1=﹣6，x2=﹣1  B． x1=0，x2=5  C． x1=﹣3，x2=5  D． x1=﹣6，x2=2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


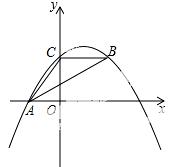
    如图，抛物线y=ax2+bx+c经过A（﹣3.0）、C（0，4），点B在抛物线上，CB∥x轴，且AB平分∠CAO．

    （1）求抛物线的解析式；

    （2）线段AB上有一动点P，过点P作y轴的平行线，交抛物线于点Q，求线段PQ的最大值；

    （3）抛物线的对称轴上是否存在点M，使△ABM是以AB为直角边的直角三角形？如果存在，求出点M的坐标；如果不存在，说明理由．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC中，点D、E分别是AB、AC的中点，CF平分∠ACB交DE于点F，若AC=8，则EF的长为__________．

     


    查看答案和解析>>

    同步练习册答案