
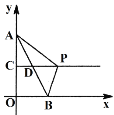
【题目】如图,点A(0,4)、B(2,0),点C、D分别是OA、AB的中点,在射线CD上有一动点P,若△ABP是直角三角形,则点P的坐标为_____.
【答案】(6,2);(1+![]() ,2).
,2).
【解析】
根据勾股定理得到AB=2![]() ,根据三角形中位线的性质得到AC=OC=2,CD=1,AD=BD=
,根据三角形中位线的性质得到AC=OC=2,CD=1,AD=BD=![]() ,①当∠APB=90°时,根据直角三角形的性质得到PD=AD=
,①当∠APB=90°时,根据直角三角形的性质得到PD=AD=![]() ,于是得到P(
,于是得到P(![]() +1,2),②当∠ABP=90°时,如图,过P作PC⊥x轴于C,根据相似三角形的性质得到BP=AB=2
+1,2),②当∠ABP=90°时,如图,过P作PC⊥x轴于C,根据相似三角形的性质得到BP=AB=2![]() ,得到PC=6,求得P(6,2).
,得到PC=6,求得P(6,2).
解:∵点A(0,4),点B(2,0),
∴OA=4,OB=2,
∴AB=2![]() ,
,
∵点C,D分别是OA,AB的中点,
∴AC=OC=2,CD=1,AD=BD=![]() ,
,
①当∠APB=90°时,
∵AD=BD,
∴PD=AD=![]() ,
,
∴PC=CD+PD=![]() +1,
+1,
∴P(![]() +1,2),
+1,2),
②当∠ABP=90°时,如图,
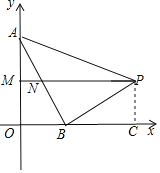
过P作PC⊥x轴于C,
则△ABO∽△BPC,![]()
∴BP=AB=2![]() ,
,
∴PC=OB=2,
∴BC=4,
∴PC=OC=2+4=6,
∴P(6,2),
故答案为:(![]() +1,2)或(6,2).
+1,2)或(6,2).


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】为了调查A、B两个区的初三学生体育测试成绩,从两个区各随机抽取了1000名学生的成绩(满分:40分,个人成绩四舍五入向上取整数)
A区抽样学生体育测试成绩的平均分、中位数、众数如下:
平均分 | 中位数 | 众数 |
37 | 36 | 37 |
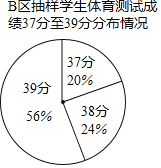
B区抽样学生体育测试成绩的分布如下:
成绩 | 28≤x<31 | 31≤x<34 | 34≤x<37 | 37≤x<40 | 40(满分) |
人数 | 60 | 80 | 140 | m | 220 |
请根据以上信息回答下列问题
(1)m= ;
(2)在两区抽样的学生中,体育测试成绩为37分的学生,在 (填“A”或“B”)区被抽样学生中排名更靠前,理由是 ;
(3)如果B区有10000名学生参加此次体育测试,估计成绩不低于34分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
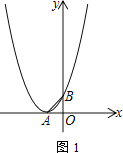
【题目】已知抛物线顶点A在x轴负半轴上,与y轴交于点B,OB=1,△OAB为等腰直角三角形
(1)求抛物线的解析式
(2)若点C在抛物线上,若△ABC为直角三角形,求点C的坐标
(3)已知直线DE过点(-1,-4),交抛物线于点D、E,过D作DF∥x轴,交抛物线于点F,求证:直线EF经过一个定点,并求定点的坐标

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种成本价为10元/kg的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不得高于18元/kg.在销售过程中发现销量y(kg)与售价x(元/kg)之间满足一次函数关系,对应关系如下表所示:
x | 12 | 14 | 15 | 17 |
y | 36 | 32 | 30 | 26 |
⑴求y与x之间的函数关系式,并写出自变量x的取值范围;
⑵若该经销商想使这种商品获得平均每天168元的利润,求售价应定为多少元/kg?
⑶设销售这种商品每天所获得的利润为W元,求W与x之间的函数关系式;并求出该商品销售单价定为多少元时,才能使经销商所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
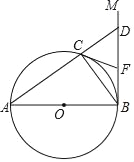
【题目】如图,AB为⊙O的直径,直线BM⊥AB于点B,点C在⊙O上,分别连接BC,AC,且AC的延长线交BM于点D,CF为⊙O的切线交BM于点F.
(1)求证:CF=DF;
(2)连接OF,若AB=10,BC=6,求线段OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题探究)小敏在学习了Rt△ABC的性质定理后,继续进行研究.
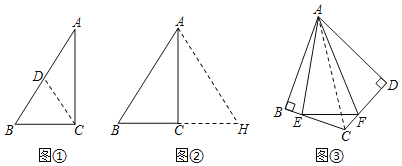
(1)(i)她发现图①中,如果∠A=30°,BC与AB存在特殊的数量关系是 ;
(ii)她将△ABC沿AC所在的直线翻折得△AHC,如图②,此时她证明了BC和AB的关系;请根据小敏证明的思路,补全探究的证明过程;
猜想:如果∠A=30°,BC与AB存在特殊的数量关系是 ;
证明:△ABC沿AC所在的直线翻折得△AHC,
(2)如图③,点E、F分别在四边形ABCD的边BC、CD上,且∠B=∠D=90°,连接AE、AF、EF,将△ABE、△ADF折叠,折叠后的图形恰好能拼成与△AEF完全重合的三角形,连接AC,若∠EAF=30°,AB2=27,则△CEF的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+c(a≠0)与y轴交于点A,将点A向右平移2个单位长度,得到点B.直线![]() 与x轴,y轴分别交于点C,D.
与x轴,y轴分别交于点C,D.
(1)求抛物线的对称轴.
(2)若点A与点D关于x轴对称.
①求点B的坐标.
②若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com