
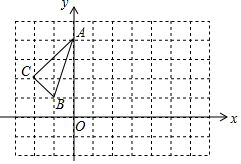
 如图,已知△ABC三个顶点的坐标分别为A(0,4),B(-1,1),C(-2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为(6,0).
如图,已知△ABC三个顶点的坐标分别为A(0,4),B(-1,1),C(-2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为(6,0).  超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
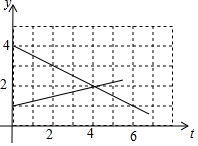 某工厂有甲、乙两个长方体的水池,甲水池较深,甲池的水用抽水机匀速地抽入乙池,如图所示的是甲、乙两个水池水的深度y(m)与抽水时间t(h)的函数关系的图象.
某工厂有甲、乙两个长方体的水池,甲水池较深,甲池的水用抽水机匀速地抽入乙池,如图所示的是甲、乙两个水池水的深度y(m)与抽水时间t(h)的函数关系的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
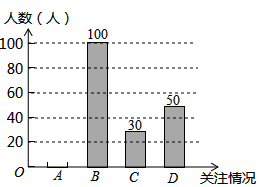 温州市政府计划投资百亿元开发瓯江口新区,打造出一个“东方时尚岛、海上新温州”.为了解温州市民对瓯江口新区的关注情况,某学校数学兴趣小组随机采访部分温州市民,对采访情况制作了统计图表的一部分如下:
温州市政府计划投资百亿元开发瓯江口新区,打造出一个“东方时尚岛、海上新温州”.为了解温州市民对瓯江口新区的关注情况,某学校数学兴趣小组随机采访部分温州市民,对采访情况制作了统计图表的一部分如下:| 关注情况 | 频数 | 频率 |
| A.高度关注 | m | 0.1 |
| B.一般关注 | 100 | 0.5 |
| C.不关注 | 30 | n |
| D.不知道 | 50 | 0.25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
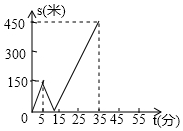 甲、乙两人匀速从同一地点到1500m处的图书馆看书,甲出发5min后乙以一定的速度沿同一路线行走.设甲、乙两人相距s(m),甲行走的时间为t(min),s为t的函数,其图象的一部分如图所示.
甲、乙两人匀速从同一地点到1500m处的图书馆看书,甲出发5min后乙以一定的速度沿同一路线行走.设甲、乙两人相距s(m),甲行走的时间为t(min),s为t的函数,其图象的一部分如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 38 | B. | 40 | C. | 42 | D. | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com