
抛物线y=2x2﹣bx+3的对称轴是直线x=1,则b的值为 .
4. 【解析】试题考查知识点:抛物线y=ax2+bx+c(a≠0)的对称轴是直线 思路分析:直接套用对称轴解析式即可得到关于系数b的方程 具体解答过程: ∵抛物线y=ax2+bx+c(a≠0)的对称轴是直线,抛物线y=2x2-bx+3的对称轴是直线x=1 ∴ 解之得:b=4科目:初中数学 来源:江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型:解答题
解方程:(1)x2 +2x –3=0; (2)x(x+1)=2(x+1).
(1)x1=-3,x2=1;(2)x1=-1,x2=2 【解析】试题分析:(1)利用十字相乘法求解即可;(2)先移项,然后利用因式分解法求解. 【解析】 (1)(x+3)(x-1)=0 x1=-3,x2=1 (2)x(x+1)-2(x+1)=0 (x+1) (x-2)=0 x1=-1,x2=2查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
运算:  ,
,  ,
,
 ,
, 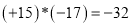 ,
,
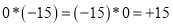 ,
,  .
.
( )请你认真思考上述运算,归纳*运算的法则:两数进行*运算时,__________.
)请你认真思考上述运算,归纳*运算的法则:两数进行*运算时,__________.
特别地,  和任何数进行*运算,或任何数和
和任何数进行*运算,或任何数和 进行*运算,__________.
进行*运算,__________.
( )计算:
)计算:  __________.
__________.
( )是否存在有理数
)是否存在有理数 、
、 ,使得
,使得 ,若存在,求出
,若存在,求出 、
、 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
下列各对数中,数值相等的是( ).
A.  和
和 B.
B. 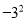 和
和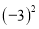 C.
C.  和
和 D.
D. 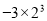 和
和
查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
有理数 的相反数是( ).
的相反数是( ).
A.  B.
B. 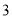 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:天津市2018届九年级(上)第四周周清数学试卷 题型:单选题
由二次函数y=﹣x2+2x可知( )
A. 图象是开口向上的 B. 对称轴为x=﹣1 C. 最大值为1 D. 顶点坐标为(﹣1,1)
C 【解析】试题解析:∵y=﹣x2+2x=﹣(x﹣1)2+1, ∴抛物线的开口向下,A错误; 对称轴为直线x=1,B错误; 当x=1时,函数取得最大值1,C正确; 顶点坐标为(1,1),D错误; 故选:C查看答案和解析>>
科目:初中数学 来源:广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
已知:多项式A=b³-2ab.
(1)请将A进行因式分解;
(2)若A=0且a≠0,b≠0,求 的值
的值
查看答案和解析>>
科目:初中数学 来源:广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列各运算中,正确的是( )
A. a³·a²=a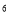 B. (-4a³)²=16a
B. (-4a³)²=16a C. a
C. a ÷a²= a³ D. (a-1)²=a²-1
÷a²= a³ D. (a-1)²=a²-1
查看答案和解析>>
科目:初中数学 来源:湖南省武冈市2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论:①∠DEF=∠DFE;②AE=AF;③DA平分∠EDF;④EF垂直平分AD.其中正确的序号是____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com