
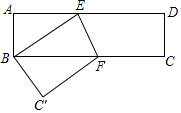
 如图,将一张长方形纸片ABCD沿EF折叠,使点D与点B重合,点C落在C'的位置上.
如图,将一张长方形纸片ABCD沿EF折叠,使点D与点B重合,点C落在C'的位置上.分析 (1)依据平行线的性质可求得∠DEF的度数,然后依据翻折的性质可求得∠BEF的度数,于是可求得∠AEB的度数.
(2)先依据翻折的性质得到BE=DE,然后设BE=DE=x,然后在△AEB中,依据勾股定理列出关于x的方程求解即可.
解答 解:(1)∵AD∥BC,
∴∠BFE=∠FED=65°.
由翻折的性质可知:∠BEF=∠DEF=65°.
∴∠AEB=180°-65°-65°=50°;
(2)由翻折的性质可知BE=DE.
设BE=DE=x,在△AEB中,依据勾股定理可知:BE2=AB2+AE2,即x2=32+(9-x)2,
解得:x=5cm.
故答案为:(1)50°;(2)5cm.
点评 本题主要考查的是翻折的性质,熟练掌握翻折的性质是解题的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com