
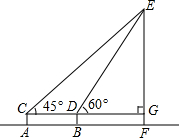
 如图,为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°,已知测角仪AC的高为1.6米,CD的长为6米,CD所在的水平线CG⊥EF于点G,铁塔EF的高为(10.6+3$\sqrt{3}$)米.(结果用带根号的式子表示)
如图,为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°,已知测角仪AC的高为1.6米,CD的长为6米,CD所在的水平线CG⊥EF于点G,铁塔EF的高为(10.6+3$\sqrt{3}$)米.(结果用带根号的式子表示) 分析 根据已知得出EG=CG,进而求出CD+DG=EG,再利用测角仪AC的高为1.6m,求出铁塔EF的高即可.
解答 解:设DG=x,得出EG=$\sqrt{3}$x,
∵∠ECG=45°,∠CGE=90°,
∴∠CEG=45°,
∴EG=CG,
∴CD+DG=EG,
∴6+x=$\sqrt{3}$x,
解得:x=3$\sqrt{3}$+3,
∴$\sqrt{3}$×(3$\sqrt{3}$+3)=(9+3$\sqrt{3}$)米,
∴EF=9+3$\sqrt{3}$+1.6=(10.6+3$\sqrt{3}$)米.
故答案为:(10.6+3$\sqrt{3}$)米.
点评 此题主要考查了解直角三角形的应用-仰角俯角问题的应用,根据已知得出EG的长是解题关键.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
 (1)实数a、b在数轴上的位置如图所示,请化简:|a|-$\sqrt{a^2}-\sqrt{b^2}$;
(1)实数a、b在数轴上的位置如图所示,请化简:|a|-$\sqrt{a^2}-\sqrt{b^2}$;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
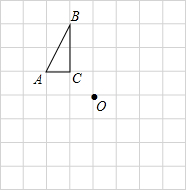 如图,每个小方格都是边长为1个单位长度的小正方形.
如图,每个小方格都是边长为1个单位长度的小正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
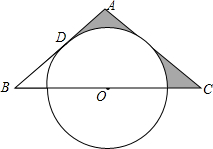 在△ABC中,AB=AC,O是BC中点,BC=12$\sqrt{3}$cm,AB与⊙O相切于点D,AD:DB=1:3
在△ABC中,AB=AC,O是BC中点,BC=12$\sqrt{3}$cm,AB与⊙O相切于点D,AD:DB=1:3查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
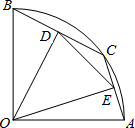 如图,在半径为4的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若四边形AOBC的面积为10,则△DOE的面积是$\frac{9}{2}$.
如图,在半径为4的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若四边形AOBC的面积为10,则△DOE的面积是$\frac{9}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com