
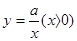 的图象与直线
的图象与直线 相交于点A(1,3)、B(
相交于点A(1,3)、B( ,1)两点,
,1)两点,
 、
、 、
、 的值;
的值; 的解(请直接写出答案);
的解(请直接写出答案);科目:初中数学 来源:不详 题型:填空题
 分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=30°,AB=4,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为 ▲ .
分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=30°,AB=4,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为 ▲ .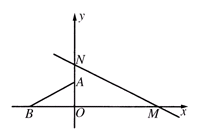
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
销售单价 (元/件) (元/件) | …… | 30 | 40 | 50 | 60 | …… |
每天销售量 (件) (件) | …… | 500 | 400 | 300 | 200 | …… |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 x的图象于点B.矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴上方,DC=2,DE=4.当点C坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
x的图象于点B.矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴上方,DC=2,DE=4.当点C坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 型号 | A | B |
| 进价(元/件) | 90 | 120 |
| 获利(元/件) | 20 | 22 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
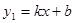 的图象与反比例函数
的图象与反比例函数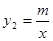 的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.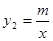 和一次函数
和一次函数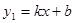 的表达式;
的表达式;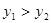 时
时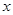 的取值范围。
的取值范围。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com