
如图,在△ABC中,∠C=90°,BC=3,AB=5.点P从点B出发,以每秒1个单位长度沿B→C→A→B的方向运动;点Q从点C出发,以每秒 2个单位沿C→A→B方向的运动,到达点B后立即原速返回,若P、Q两点同时运动,相遇后同时停止,设运动时间为t秒.
2个单位沿C→A→B方向的运动,到达点B后立即原速返回,若P、Q两点同时运动,相遇后同时停止,设运动时间为t秒.
(1)当t= 时,点P与点Q相遇;
(2)在点P从点B到点C的运动过程中,当ι为何值时,△PCQ为等腰三角形?
(3)在点Q从点B返回点A的运动过程中,设△PCQ的面积为s平方单位.求s与ι之间的函数关系式;
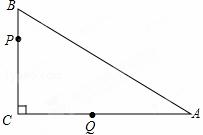
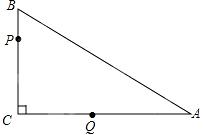
|
解:(1)7
(2)Q从C到A的时间是2秒,P从A到C的时间是3秒.
则当0≤t≤2时,若△PCQ为等腰三角形,则一定有:PC=CQ,
即3﹣t=2t,解得:t=1
当2<t≤3时,若△PCQ为等腰三角形,则一定有PQ=QC(如图1).则Q在PC的中垂线上,作QH⊥AC,则QH=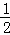 PC.△AQH∽△ABC,
PC.△AQH∽△ABC,
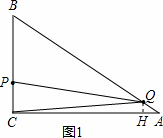 在直角△AQH中,AQ=2t﹣4,则QH=
在直角△AQH中,AQ=2t﹣4,则QH=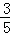 AQ=
AQ=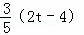
∵PC=BC﹣BP=3﹣t,
∴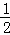 ×
×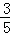 (2t﹣4)=3﹣t,
(2t﹣4)=3﹣t,
解得:t=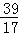 ;
;
综上:当t=1或t=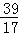 时△PCQ为等腰三角形-
时△PCQ为等腰三角形-
(3)在点Q从点B返回点A的运动过程中,P一定在AC上,则PC=t﹣3,BQ=2t﹣9,
即AQ=5﹣(2t﹣9)=14﹣2t.
同(2)可得:△PCQ中,PC边上的高是: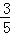 (14﹣2t),
(14﹣2t),
故s=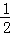 (t﹣3)×
(t﹣3)×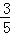 (14﹣2t)=
(14﹣2t)=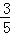 (﹣t2+10t﹣21).
(﹣t2+10t﹣21).


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
任何实数a,可用 表示不超过a的最大整数,如
表示不超过a的最大整数,如 ,现对72进行如下操作:
,现对72进行如下操作:
 ,
,
这样对72只需进行3次操作后变为1,类似地,①对81只需进行 次操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△OAB中,点B的坐标是(0,4),点A的坐标是(3,1).画出△OAB绕点B顺时针旋转90°后的△BA1O1,求出点A1的坐标,并求出点A旋转到A1所经过的路径长(结果保留 )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
在平面中,下列命题为真命题的是( )
A.四边相等的四边形是正方形 B.四个角相等的四边形是矩形
C.对角线相等的四边形是菱形 D.对角线互相垂直的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,抛物线 与
与 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与 轴交于点C,点B的坐标为(3,0),将直线
轴交于点C,点B的坐标为(3,0),将直线 沿
沿 轴向上平移3个单位长度后恰好经过B、C两点。
轴向上平移3个单位长度后恰好经过B、C两点。
(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且 ,求点P的坐标。
,求点P的坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,AB =10 ,AC =8 , BC =6 ,经过点C且与边 相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是………………( )
相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是………………( )
A. B.
B. C.
C. D.
D.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com