
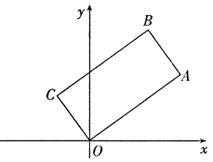
【题目】如图,在矩形![]() 中,
中, ![]() ,顶点
,顶点![]() 在坐标原点,顶点
在坐标原点,顶点![]() 的坐标为(8,6).
的坐标为(8,6).
(1)顶点![]() 的坐标为( , ),顶点
的坐标为( , ),顶点![]() 的坐标为( , );
的坐标为( , );
(2)现有动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,点
同时出发,点![]() 沿线段
沿线段![]() 向终点
向终点![]() 运动,速度为每秒2个单位,点
运动,速度为每秒2个单位,点![]() 沿折线
沿折线![]() →
→![]() →
→![]() 向终点
向终点![]() 运动,速度为每秒
运动,速度为每秒![]() 个单位.当运动时间为2秒时,以点
个单位.当运动时间为2秒时,以点![]() 、
、![]() 、
、![]() 顶点的三角形是等腰三角形,求
顶点的三角形是等腰三角形,求![]() 的值.
的值.
(3)若矩形![]() 以每秒
以每秒![]() 个单位的速度沿射线
个单位的速度沿射线![]() 下滑,直至顶点
下滑,直至顶点![]() 到达坐标原点时停止下滑.设矩形
到达坐标原点时停止下滑.设矩形![]() 在
在![]() 轴下方部分的面积为
轴下方部分的面积为![]() ,求
,求![]() 关于滑行时间
关于滑行时间![]() 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量![]() 的取值范围.
的取值范围.
【答案】(1)顶点C的坐标为![]() ,顶点B的坐标为
,顶点B的坐标为![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)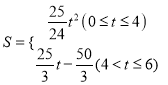 .
.
【解析】试题分析:(1) 连接AC、OB,过点C作CE![]() x轴, AD
x轴, AD![]() x轴,利用矩形的性质,证明
x轴,利用矩形的性质,证明![]() ,所以可得到B,C坐标.(2) 分类讨论,当PQ=CQ时,过点Q作QD
,所以可得到B,C坐标.(2) 分类讨论,当PQ=CQ时,过点Q作QD ![]() ,垂足为D,求出k值,当CP=CQ时,OQ+OA=11,求出k值,(3)分类讨论,当:当0
,垂足为D,求出k值,当CP=CQ时,OQ+OA=11,求出k值,(3)分类讨论,当:当0![]() 时.,可求出
时.,可求出![]() 关于滑行时间
关于滑行时间![]() 的函数关系式,当4
的函数关系式,当4![]() 时.过点C′作C′E
时.过点C′作C′E ![]() ,求出函数关系式
,求出函数关系式
试题解析:
解:(1)如图1所示:连接AC、OB,过点C作CE![]() x轴, AD
x轴, AD![]() x轴,
x轴,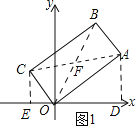
![]() A(8,6),AD=6,OD=8, CE
A(8,6),AD=6,OD=8, CE![]() x轴, AD
x轴, AD![]() x,
x,
∠CEO=∠ADO,
![]() 是矩形,
是矩形,![]()
, ![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,![]() 为矩形,F为AC、OB的中点.
为矩形,F为AC、OB的中点.
设点B的坐标为![]() (x,y).则,计算得出:x=5,y=10,
(x,y).则,计算得出:x=5,y=10,
点B的坐标为(5,10).![]() 答案是: C(-3,4),B(5,10)
答案是: C(-3,4),B(5,10)
(2)![]() 由两点间的距离公式可以知道:,OA=10,
由两点间的距离公式可以知道:,OA=10,![]() PC=4,
PC=4,
![]() PQ>PC.
PQ>PC.
如图2所示:V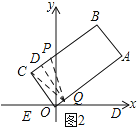
, ![]()
![]()
![]() ,
,![]() 四边形CDQO为矩形.
四边形CDQO为矩形.![]() OQ=CD=2,
OQ=CD=2,
AQ=8, ![]() k=2.
k=2.
如图3所示:当CP=CQ时,OQ+OA=11.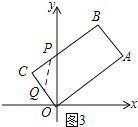
则k=![]() .
.
综上所述,当k=4或k=![]() .时,
.时, ![]() CQP为等腰三角形.
CQP为等腰三角形.
(3)如图4所示:当0![]() 时.
时.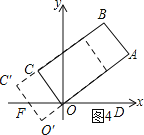
![]() ,
,
∴tan∠FOO’=![]() ,OO’=
,OO’=![]() ,
,
∴FO’=![]() ∴S=
∴S=![]() .
.
如图5所示:当4![]() 时.过点C′作C′E
时.过点C′作C′E ![]()
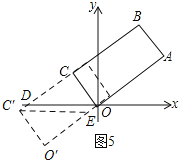
![]() tan∠CEO′=
tan∠CEO′=![]() ,O′C′=5,
,O′C′=5,
∴O’E=![]() ,C’D=
,C’D=![]() ,
,
∴S=![]() O’C’(C’D+O’E)=
O’C’(C’D+O’E)= ![]() .
.
综上所述,S与t的关系式为
S=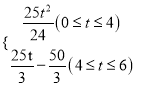 ,
,


科目:初中数学 来源: 题型:
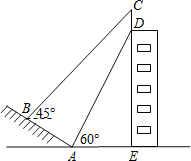
【题目】如图,山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:
,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条东西走向的商业街上,依次有书店(记为A)、冷饮店(记为B)、鞋店(记为C),冷饮店位于鞋店西边50m处,鞋店位于书店东边60m处,王平先去书店,然后沿着这条街向东走了30m至D处,接着向西走50m到达E处.
(1)以A为原点、向东为正方向画数轴,在数轴上表示出上述A,B,C,D,E的位置;
(2)若在这条街上建一家超市,使超市与鞋店C分居E点两侧,且到E点的距离相等,问超市在冷饮店的什么方向?距离多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
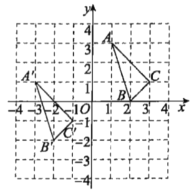
【题目】三角形ABC与三角形![]() 在平面直角坐标系中的位置如图所示,三角形
在平面直角坐标系中的位置如图所示,三角形![]() 是由三角形ABC经过平移得到的.
是由三角形ABC经过平移得到的.
(1)分别写出点![]()
![]()
![]() 的坐标;
的坐标;
(2)说明三角形![]() 是由三角形ABC经过怎样的平移得到的;
是由三角形ABC经过怎样的平移得到的;
(3)若点![]() 是三角形ABC内的一点,则平移后点P在三角形
是三角形ABC内的一点,则平移后点P在三角形![]() 内的对应点为P‘,写出点P’的坐标.
内的对应点为P‘,写出点P’的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.

(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠DPF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
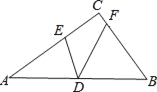
【题目】如图,在△ABC中,∠ACB=90°,D为边AB的中点,E,F分别为边AC,BC上的点,且AE=AD,BF=BD.若DE=2![]() ,DF=4,则AB的长为_____.
,DF=4,则AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD的中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF,
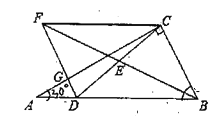
(1)求证:四边形DBCF是平行四边形
(2)若∠A=30°,BC=4,CF=6,求CD的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com