
【题目】如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°. 
(1)求证:AC是⊙O的切线;
(2)求图中阴影部分的面积.
【答案】
(1)证明:连接OC,

由圆周角定理得,∠BOC=2∠CDB=60°,
∵∠OBD=30°,
∴OC⊥BD,
∵AC∥BD,
∴OC⊥AC,
∴AC是⊙O的切线;
(2)解:扇形OBC的面积= ![]() =6π,
=6π,
∵OB=6,∠OBH=30°,
∴OH=3,BH=3 ![]() ,
,
△OBH的面积= ![]() ×BH×OH=
×BH×OH= ![]() ×3
×3 ![]() ×3=
×3= ![]()
![]() ,
,
△HCD的面积= ![]() ×6×3
×6×3 ![]() ×
× ![]() =
= ![]()
![]() ,
,
∴阴影部分的面积=6π﹣ ![]()
![]() +
+ ![]()
![]() =6π.
=6π.
【解析】(1)连接OC,根据圆周角定理得到∠BOC=2∠CDB=60°,得到OC⊥BD,根据平行线的性质得到OC⊥AC,根据切线的判定定理证明结论;(2)根据扇形的面积公式、三角形的面积公式计算即可.
【考点精析】本题主要考查了切线的判定定理和扇形面积计算公式的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】发现与探究:如图,△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=45°,点B,C,E三点共线,且BC:CE=2:1,连接AE,BD. 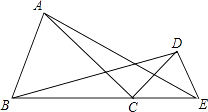
(1)在不添加辅助线和字母的情况下,请在图中找出一对全等三角形(用“≌”表示),并加以证明;
(2)求tan∠BDC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
(1)根据表中数据在平面直角坐标系中描出实数x,y的对应点,用平滑曲线连接这些点,并观察所得的图像,猜测y与x之间的函数关系,并求出该函数关系式:
x(元) | 3 | 4 | 5 | 6 |
y(个) | 20 | 15 | 12 | 10 |

(2)设经营此笔记本的日销售利润为w元,试求出w与x之间的函数关系式;
(3)当日销售单价为8元时,求日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC=12,BD=8,P是AC上的一个动点,过点P作EF∥BD,与平行四边形的两条边分别交于点E、F.设CP=x,EF=y,则下列图像中,能表示y与x的函数关系的图像大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABO中,∠ABO=90°,OB边在x轴上,将△ABO绕点B顺时针旋转60°得到△CBD.若点A的坐标为(﹣2,2 ![]() ),则点C的坐标为( )
),则点C的坐标为( )
A.( ![]() ,1)
,1)
B.(1, ![]() )
)
C.(1,2)
D.(2,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+1(a<0)的图象过点(1,0)和(x1 , 0),且﹣2<x1<﹣1,下列5个判断中:①b<0;②b﹣a<0;③a>b﹣1;④a<﹣ ![]() ;⑤2a<b+
;⑤2a<b+ ![]() ,正确的是( )
,正确的是( )
A.①③
B.①②③
C.①②③⑤
D.①③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com