
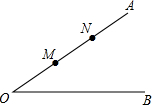
 如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是x=0或x=4$\sqrt{2}$-4或4<x<4$\sqrt{2}$.
如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是x=0或x=4$\sqrt{2}$-4或4<x<4$\sqrt{2}$. 分析 分三种情况讨论:先确定特殊位置时成立的x值,
①如图1,当M与O重合时,即x=0时,点P恰好有三个;
②如图2,构建腰长为4的等腰直角△OMC,和半径为4的⊙M,发现M在点D的位置时,满足条件;
③如图3,根据等腰三角形三种情况的画法:分别以M、N为圆心,以MN为半径画弧,与OB的交点就是满足条件的点P,再以MN为底边的等腰三角形,通过画图发现,无论x取何值,以MN为底边的等腰三角形都存在一个,所以只要满足以MN为腰的三角形有两个即可.
解答 解:分三种情况:
①如图1,当M与O重合时,即x=0时,点P恰好有三个;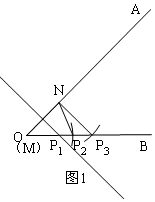
②如图2,以M为圆心,以4为半径画圆,当⊙M与OB相切时,设切点为C,⊙M与OA交于D,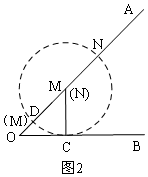
∴MC⊥OB,
∵∠AOB=45°,
∴△MCO是等腰直角三角形,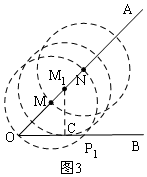
∴MC=OC=4,
∴OM=4$\sqrt{2}$,
当M与D重合时,即x=OM-DM=4$\sqrt{2}$-4时,同理可知:点P恰好有三个;
③如图3,取OM=4,以M为圆心,以OM为半径画圆,
则⊙M与OB除了O外只有一个交点,此时x=4,即以∠PMN为顶角,MN为腰,符合条件的点P有一个,以N圆心,以MN为半径画圆,与直线OB相离,说明此时以∠PNM为顶角,以MN为腰,符合条件的点P不存在,还有一个是以NM为底边的符合条件的点P;
点M沿OA运动,到M1时,发现⊙M1与直线OB有一个交点;
∴当4<x<4$\sqrt{2}$时,圆M在移动过程中,则会与OB除了O外有两个交点,满足点P恰好有三个;
综上所述,若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是:x=0或x=4$\sqrt{2}$-4或4$<x<4\sqrt{2}$.
故答案为:x=0或x=4$\sqrt{2}$-4或4$<x<4\sqrt{2}$.
点评 本题考查了等腰三角形的判定,有难度,本题通过数形结合的思想解决问题,解题的关键是熟练掌握已知一边,作等腰三角形的画法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
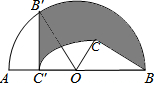 如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为πcm2.
如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为πcm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16(1+2x)=25 | B. | 25(1-2x)=16 | C. | 16(1+x)2=25 | D. | 25(1-x)2=16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
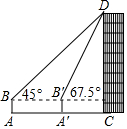 如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米,$\sqrt{2}$≈1.414)( )
如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米,$\sqrt{2}$≈1.414)( )| A. | 34.14米 | B. | 34.1米 | C. | 35.7米 | D. | 35.74米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
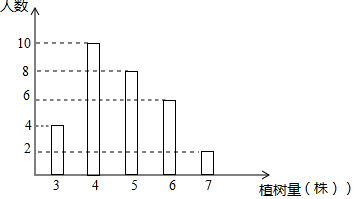
| A. | 参加本次植树活动共有30人 | B. | 每人植树量的众数是4棵 | ||
| C. | 每人植树量的中位数是5棵 | D. | 每人植树量的平均数是5棵 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>0>y2 | B. | y2>0>y1 | C. | y1>y2>0 | D. | y2>y1>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
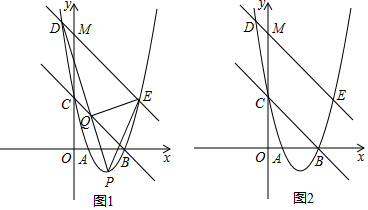
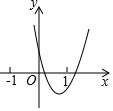 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y=$\frac{a-b+c}{x}$在同一坐标系中的大致图象是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y=$\frac{a-b+c}{x}$在同一坐标系中的大致图象是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com