
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 解方程组后代入代数式解答即可.
解答 解:$\left\{\begin{array}{l}{x+2y=1①}\\{y+2z=2②}\\{2x+z=3③}\end{array}\right.$,
把①变形为:x=1-2y④,
把④代入③得:-4y+z=1⑤,
②-⑤×2得:y=0,
把y=0代入④得:x=1,
把x=1代入③得:z=1,
所以方程组的解是:$\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=1}\end{array}\right.$,
把x=1,y=0,z=1代入x+y+z=2.
故选C
点评 此题考查方程组,关键是根据三元一次方程组进行计算后代入代数式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
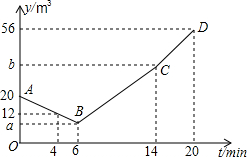 水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.
水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.| 时间 | 池中有水(m3) |
| 12:00 | 20 |
| 12:04 | 12 |
| 12:06 | a |
| 12:14 | b |
| 12:20 | 56 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
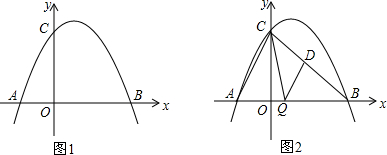
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y2<y1<y3 | D. | y3<y1<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图在直角平面坐标系xOy中,OA=OC=3OB,二次函数y=-x2+bx+c的图象经过A、B、C.
如图在直角平面坐标系xOy中,OA=OC=3OB,二次函数y=-x2+bx+c的图象经过A、B、C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com