
【题目】如图,在等腰Rt△ABC中,AC=BC=2 ![]() ,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( ) 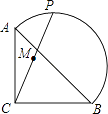
A.![]() π
π
B.π
C.2 ![]()
D.2
【答案】B
【解析】解:取AB的中点O、AC的中点E、BC的中点F,连结OC、OP、OM、OE、OF、EF,如图, ∵在等腰Rt△ABC中,AC=BC=2 ![]() ,
,
∴AB= ![]() BC=4,
BC=4,
∴OC= ![]() AB=2,OP=
AB=2,OP= ![]() AB=2,
AB=2,
∵M为PC的中点,
∴OM⊥PC,
∴∠CMO=90°,
∴点M在以OC为直径的圆上,
点P点在A点时,M点在E点;点P点在B点时,M点在F点,易得四边形CEOF为正方形,EF=OC=2,
∴M点的路径为以EF为直径的半圆,
∴点M运动的路径长= ![]() 2π1=π.
2π1=π.
故选B.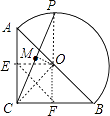
【考点精析】通过灵活运用等腰直角三角形,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°即可以解答此题.


科目:初中数学 来源: 题型:
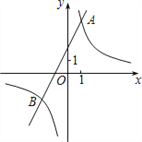
【题目】如图,已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2)。
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2)。
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1<y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,抛物线 ![]() 与
与 ![]() 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足
轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足 ![]() ,则称点P为抛物线
,则称点P为抛物线 ![]() 的勾股点。
的勾股点。

(1)直接写出抛物线 ![]() 的勾股点的坐标;
的勾股点的坐标;
(2)如图2,已知抛物线C: ![]() 与
与 ![]() 轴交于A,B两点,点P(1,
轴交于A,B两点,点P(1, ![]() )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件 ![]() 的点Q(异于点P)的坐标
的点Q(异于点P)的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线![]() 相交于点
相交于点![]() 于点
于点![]() 于点F,连结
于点F,连结![]() ,则下列结论:
,则下列结论:![]() ;
;![]() ;
;![]() ;
;![]() 图中共有四对全等三角形
图中共有四对全等三角形![]() 其中正确结论的个数是
其中正确结论的个数是![]()

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为90.
![]()
(1)请写出与A,B两点距离相等的M点对应的数;
(2)现在有一只电子蚂蚁P从B点出发时,以3个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以2个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,求C点对应的数是多少.
(3)若当电子蚂蚁P从B点出发时,以3个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以2个单位/秒的速度向右运动,求经过多长的时间两只电子蚂蚁在数轴上相距35个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连结四边形各边中点所得的四边形是矩形,则原四边形( )
A. 一定是矩形 B. 一定是菱形 C. 对角线一定相等 D. 对角线一定互相垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
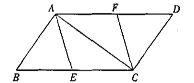
【题目】如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动.设该机器人每秒钟前进或后退1步,并且每步的距离是1个单位长,![]() 表示第n秒时机器人在数轴上的位置所对应的数.给出下列结论:①
表示第n秒时机器人在数轴上的位置所对应的数.给出下列结论:①![]()
![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,⑤
,⑤![]() ,其中正确的结论有( )
,其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com