
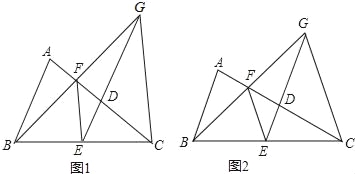
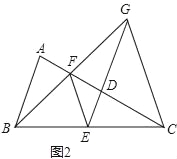
【题目】如图,已知等腰△ABC中,AC=BC,点D、E、F分别是线段AC、BC、AD的中点,连接FE、ED,BF的延长线交ED的延长线于点G,连接GC.
(1)求证:EF∥CG;
(2)若AC=![]() AB,求证:AC=CG;
AB,求证:AC=CG;
(3)如图2,若CG=EG,则![]() = .
= .
【答案】(1)证明见解析;
(2)证明见解析;
(3)![]()
【解析】
试题分析:(1)由点D、E分别是线段AC、BC的中点可得出DE为△ABC的中位线,根据中位线的性质即可得出∠CDE=∠A,进而可得出∠FDG=∠A,由此即可证出△ABF≌△DGF(ASA),根据全等三角形的性质即可得出BF=GF,即点F为线段BG的中点,再根据中位线的性质即可得出EF∥CG;
(2)过点C作CM⊥AB于点M,根据边与边的关系找出比例关系![]() =
=![]() =
=![]() ,由此即可得出△BAF∽△CAM,进而得出CF⊥BG,再由点F为线段BG的中点即可得出BC=CG,通过等量代换即可证出AC=CG;
,由此即可得出△BAF∽△CAM,进而得出CF⊥BG,再由点F为线段BG的中点即可得出BC=CG,通过等量代换即可证出AC=CG;
(3)根据DE∥AB即可得出∠GEC=∠CBA,结合两三角形为等腰三角形即可得出△GEC∽△CBA,再根据相似三角形的性质即可得出![]() ,代入数据即可得出结论.
,代入数据即可得出结论.
试题解析:(1)∵点D、E分别是线段AC、BC的中点,∴DE为△ABC的中位线,
∴DE∥AB,∴∠CDE=∠A.∵∠CDE=FDG,∴∠FDG=∠A.
∵点F为线段AD的中点,∴AF=DF.
在△ABF和△DGF中,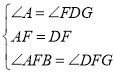 ,
,
∴△ABF≌△DGF(ASA),∴BF=GF,∴点F为线段BG的中点,
∵点E为线段BC的中点,∴EF为△BCG的中位线,∴EF∥CG.
(2)在图1中,过点C作CM⊥AB于点M.∵AC=BC,
∴AM=BM=![]() AB.∵AC=
AB.∵AC=![]() AB,
AB,
∴![]() =
=![]() =
=![]() .∵AF=
.∵AF=![]() AD=
AD=![]() AC=
AC=![]() AB,∴
AB,∴![]() =
=![]() =
=![]() ,
,
∴△BAF∽△CAM,∴∠AFB=∠AMC=90°,∴CF⊥BG.
∵点F为线段BG的中点,∴BC=CG,又∵AC=BC,∴AC=CG.
(3)∵DE为△ABC的中位线,∴DE=![]() AB,CE=
AB,CE=![]() BC=
BC=![]() AC,∵DG=AB,EG=DE+DG,
AC,∵DG=AB,EG=DE+DG,
∴EG=![]() AB.∵DE∥AB,∴∠GEC=∠CBA,∵AC=BC,CG=EG,
AB.∵DE∥AB,∴∠GEC=∠CBA,∵AC=BC,CG=EG,
∴△GEC∽△CBA,∴![]() ,既
,既 ,∴
,∴![]()
故答案为:![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
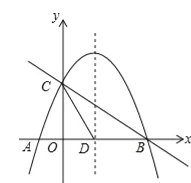
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?求出△CBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆直辖十年以来,全市投入环保资金约3 730 000万元,那么3 730 000万元用科学记数法表示为( )
A.37.3×105万元
B.3.73×106万元
C.0.373×107万元
D.373×104万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月9日是第29个“消防宣传日”.某校举行“安全小能手”消防安全知识竞赛,有50位同学参加比赛,比赛结束后根据每个学生的最后得分计算出平均数、中位数、众数和方差,如果去掉一个最高分和一个最低分,则一定不发生变化的是( ).
A.平均数B.中位数C.众数D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“※”定义新运算:对于有理数a、b都有:a※b=ab-(a+b),那么5※3=__________;当m为有理数时,3※(m※2)=____________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】满足下列哪种条件时,能判定△ABC与△DEF全等的是( )
A. ∠A=∠E, AB=EF, ∠B=∠D B. AB=DE, BC=EF, ∠C=∠F
C. AB=DE, BC=EF, ∠A=∠E, D. ∠A=∠D, AB=DE, ∠B=∠E
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com