
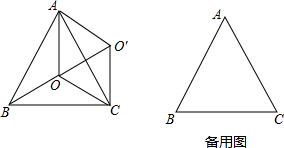
分析 将△ABO绕点A逆时针旋转60°,此时B点与C点重合,O落在O′,连接AO′、OO′、CO′,先证得△AOO′是一个等边三角形,得出∠AOO′=∠AO′O=60°,进而得到∠O′OC=∠OO′C=60°,证得△OCO′是等边三角形,因为OB=O′C,AO=OO′,所以线段OA、OB、OC构成了△OCO′,即可证得结论.
解答 证明:将△ABO绕点A逆时针旋转60°,此时B点与C点重合,O落在O′,连接AO′、OO′、CO′,
∴AO=AO′,∠OAO′=60°,
∴△AOO′是一个等边三角形,
∴AO=OO′,
又∵OB=O′C,
∴线段OA、OB、OC构成了△OCO′,
∵∠AOB=120°,∠BOC=120°.
∴∠AOC=120°,∠AO′C=120°
∵△AOO′是一个等边三角形,
∴∠AOO′=∠AO′O=60°,
∴∠O′OC=∠OO′C=60°,
∴△OCO′是等边三角形,
∴线段AO、BO、CO构成的一个三角形是等边三角形.
点评 本题考查了旋转的性质,等边三角形的判定和性质,熟练掌握性质定理是解题的关键.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
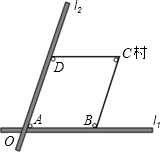 如图,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D.已知AB=BC=CD=DA=5公里,村庄C到公路l1的距离为4公里,则村庄C到公路l2的距离是( )
如图,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D.已知AB=BC=CD=DA=5公里,村庄C到公路l1的距离为4公里,则村庄C到公路l2的距离是( )| A. | 3km | B. | 4km | C. | 5km | D. | 6km |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
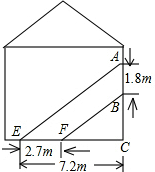 如图,阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区,已知亮区到窗口下的墙脚距离EC=7.2m,窗口高AB=1.8m.求窗口底边离地面的高BC.
如图,阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区,已知亮区到窗口下的墙脚距离EC=7.2m,窗口高AB=1.8m.求窗口底边离地面的高BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com