【题目】如图，在
中，
，
，
，点O是AB的三等分点，半圆O与AC相切，M，N分别是BC与半圆弧上的动点，则MN的最小值和最大值之和是（ ）
A. 5B. 6C. 7D. 8
心算口算巧算一课一练系列答案
应用题作业本系列答案科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，AE平分∠DAB，已知CE＝6，BE＝8，DE＝10．
（1）求BC的长；
（2）若∠CBE＝36°，求∠ADC．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在O中，弦BC垂直于半径OA，垂足为E，D是优弧BC上一点，连接BD，AD，OC，∠ADB=30°.
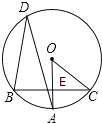
(1)求∠AOC的度数.
(2)若弦BC=8cm，求图中劣弧BC的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)问题发现
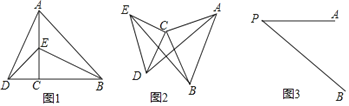
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.
填空:线段AD,BE之间的关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.
(3)解决问题
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图一座拱桥的示意图，已知桥洞的拱形是抛物线.当水面宽为12m时，桥洞顶部离水面4m.、
（1）建立平面直角坐标系，并求该抛物线的函数表达式；
（2）若水面上升1m，水面宽度将减少多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1（注：与图2完全相同），在直角坐标系中，抛物线经过点三点
,
,
．
（1）求抛物线的解析式和对称轴；
（2）
是抛物线对称轴上的一点，求满足
的值为最小的点坐标（请在图1中探索）；
（3）在第四象限的抛物线上是否存在点
，使四边形
是以
为对角线且面积为
的平行四边形？若存在，请求出点坐标，若不存在请说明理由.（请在图2中探索）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB＝6
，BC＝3动点P从点A出发，沿AC以每秒4个单位长度的速度向终点C运动．过点P（不与点A、C重合）作EF⊥AC，交AB或BC于点E，交AD或DC于点F，以EF为边向右作正方形EFGH设点P的运动时间为t秒．
（1）①AC＝ ．②当点F在AD上时，用含t的代数式直接表示线段PF的长 ．
（2）当点F与点D重合时，求t的值．
（3）设方形EFGH的周长为l，求l与t之间的函数关系式．
（4）直接写出对角线AC所在的直线将正方形EFGH分成两部分图形的面积比为1：2时t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个不透明的布袋中装有4个只有颜色不同的球，其中1个黄球、1个蓝球、2个红球．
（1）任意摸出1个球，记下颜色后不放回，再任意摸出1个球．求两次摸出的球恰好都是红球的概率（要求画树状图或列表）；
（2）现再将n个黄球放入布袋，搅匀后，使任意摸出1个球是黄球的概率为
，求n的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某生产商存有1200千克
产品，生产成本为150元/千克，售价为400元千克.因市场变化，准备低价一次性处理掉部分存货，所得货款全部用来生产
产品，产品售价为200元/千克.经市场调研发现，产品存货的处理价格
（元/千克）与处理数量
（千克）满足一次函数关系（
），且得到表中数据.
|
|
200 | 350 |
400 | 300 |
（1）请求出处理价格（元千克）与处理数量（千克）之间的函数关系；
（2）若产品生产成本为100元千克，产品处理数量为多少千克时，生产产品数量最多，最多是多少？
（3）由于改进技术，产品的生产成本降低到了
元/千克，设全部产品全部售出，所得总利润为
（元），若
时，满足随的增大而减小，求的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
