
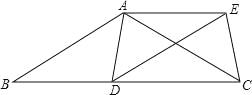
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
【答案】(1)证明见解析;
(2)点D在BC的中点上时,四边形ADCE是矩形.
【解析】
试题分析:(1)利用等边对等角以及平行四边形的性质可以证得∠EDC=∠ACB,则易证△ADC≌△ECD,利用全等三角形的对应边相等即可证得;
(2)根据平行四边形性质推出AE=BD=CD,AE∥CD,得出平行四边形,根据AC=DE推出即可.
试题解析:(1)证明:∵AB=AC,∴∠B=∠ACB,又∵ABDE中,AB=DE,AB∥DE,
∴∠B=∠EDC=∠ACB,AC=DE,
在△ADC和△ECD中, ,
,
∴△ADC≌△ECD(SAS).
(2)点D在BC的中点上时,四边形ADCE是矩形,∵四边形ABDE是平行四边形,
∴AE=BD,AE∥BC,∵D为边长中点,∴BD=CD,∴AE=CD,AE∥CD,
∴四边形ADCE是平行四边形,∵△ADC≌△ECD,∴AC=DE,
∴四边形ADCE是矩形,即点D在BC的中点上时,四边形ADCE是矩形.


科目:初中数学 来源: 题型:
【题目】我市某工艺品厂生产一款工艺品,已知这款工艺品的生产成本为每件60元,经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系.
售价x(元) | … | 70 | 90 | … |
销售量y(件) | … | 3000 | 1000 | … |
(1)求销售量y(件)与售价x(元)之间的函数表达式.
(2)当售价为80元时,工艺品厂每天获得的利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题探究】
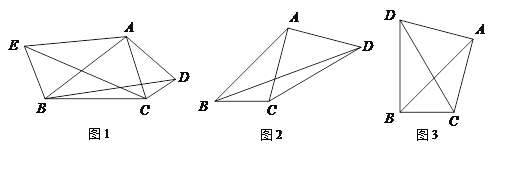
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,四边形ABCD中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45,求BD的长.
(3)如图3,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
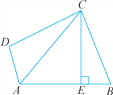
【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④AB-AD=2BE.其中正确的是( )
A. ② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究:
(1)动手操作:
①如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC∥EF,已知∠A=30°,则∠ABD+∠ACD=
②如图2,若直角三角板ABC不动,改变等腰直角三角板DEF的位置,使三角板DEF的两条直角边DE、DF仍然分别经过点B、C,那么∠ABD+∠ACD= 
(2)猜想证明:
如图3,∠BDC与∠A、∠B、∠C之间存在着 关系
(3)灵活应用:
请你直接利用以上结论,解决以下列问题:
①如图4,BE平分∠ABD,CE平分∠ACB,若∠BAC=40°,∠BDC=120°,∠BEC
②如图5,∠ABD,∠ACD的10等分线相交于点F1、F2、…、F9 ,
若∠BDC=120°,∠BF3C=64°,则∠A的度数为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.减去一个数等于加上这个数
B.两个相反数相减得0
C.两个数相减,差一定小于被减数
D.两个数相减,差不一定小于被减数
查看答案和解析>>
科目:初中数学 来源: 题型:
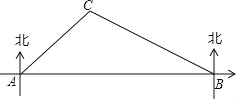
【题目】如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=400m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com