
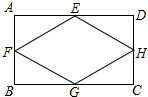
 如图,E、F、G、H分别为矩形ABCD四边的中点.
如图,E、F、G、H分别为矩形ABCD四边的中点.分析 根据矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,利用三角形中位线定理求证EF=GH=FG=EH,然后利用四条边都相等的平行四边形是菱形即可判定.
解答 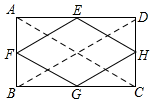 解:(1)四边形EFGH是菱形.
解:(1)四边形EFGH是菱形.
故答案为:菱形;
(2)连接BD,AC.
∵矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,
∴AC=BD,
∵EF为△ABD的中位线,
∴EF=$\frac{1}{2}$BD,EF∥BD,
又GH为△BCD的中位线,
∴GH=$\frac{1}{2}$BD,GH∥BD,
∴GH∥EF,GH=EF
同理FG为△ABC的中位线,
∴FG=$\frac{1}{2}$AC,FG∥AC,
EH为△ACD的中位线,
∴EH=$\frac{1}{2}$AC,EH∥AC,
∴EF=GH=FG=EH,
∴四边形EFGH是菱形.
点评 此题主要考查学生对菱形的判定、三角形中位线定理、和矩形的性质的理解和掌握,证明此题的关键是熟练的利用三角形中位线定理,难度不大.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
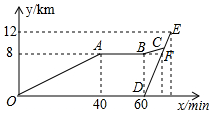 五一假期,小明骑自行车到松花江边游玩,从家出发40min后到达江边大塔,游玩一段时间后按原速度继续前往码头,在小明出发60min后,爸爸驱车沿相同路线前往码头,行驶8min时恰好经过江边大塔,如图是他们离开家的路程y(单位:km)关于小明离家时间x(单位:min)的函数图象.
五一假期,小明骑自行车到松花江边游玩,从家出发40min后到达江边大塔,游玩一段时间后按原速度继续前往码头,在小明出发60min后,爸爸驱车沿相同路线前往码头,行驶8min时恰好经过江边大塔,如图是他们离开家的路程y(单位:km)关于小明离家时间x(单位:min)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图所示,
已知:如图所示,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
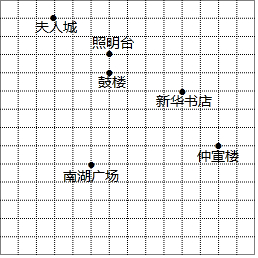 周末,小红、小丽、芳芳三位同学相约到仲宣楼游玩,出发前,她们每人带了一张用平面直角坐标系画的示意图,其中新华书店的坐标是(4,-1),南湖广场的坐标是(-1,-5).
周末,小红、小丽、芳芳三位同学相约到仲宣楼游玩,出发前,她们每人带了一张用平面直角坐标系画的示意图,其中新华书店的坐标是(4,-1),南湖广场的坐标是(-1,-5).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
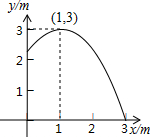 如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )
如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )| A. | 2.1m | B. | 2.2m | C. | 2.3m | D. | 2.25m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com