
 唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:
唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:分析 (1)设壶中原有x升酒,由在第3个店里遇到朋友正好喝光了壶中的酒可得出关于x的一元一次方程,解之即可得出结论;
(2)①根据a1、a2、a3的变化,找出变化规律“an=2an-1-5=2na0-(2n-1)×5”,此题得解;
②令an=2an-1-5=2na0-(2n-1)×5中n=4、an=0即可得出关于a0的一元一次方程,解之即可得出结论.
解答 解:(1)设壶中原有x升酒,
根据题意得:2[2(2x-5)-5]=5,
解得:x=$\frac{35}{8}$.
答:壶中原有$\frac{35}{8}$升酒.
(2)①观察,发现:a1=2a0-5,a2=2a1-5=22a0-(22-1)×5,a2=2a1-5=22a0-(22-1)×5,a3=2a2-5=23a0-(23-1)×5,…,
∴an=2an-1-5=2na0-(2n-1)×5.
故答案为:2an-1-5;2na0-(2n-1)×5.
②由题意得:a4=24a0-(24-1)×5=16a0-75=0,
解得:a0=$\frac{75}{16}$.
答:如果在第4个店喝光了壶中酒,则壶中原有$\frac{75}{16}$升酒.
点评 本题考查了一元一次方程的应用以及规律型中数字变化类,根据等式的变化找出变化规律是解题的关键.


科目:初中数学 来源: 题型:解答题
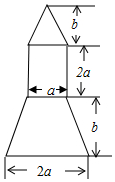 2016年10月17日7时30分,神舟十一号飞船顺利升空,同学们倍受鼓舞,开展了火箭模型制作比赛,如图示是火箭模型的截面图,下面是等腰梯形,中间是长方形,上面是一个等腰三角形.
2016年10月17日7时30分,神舟十一号飞船顺利升空,同学们倍受鼓舞,开展了火箭模型制作比赛,如图示是火箭模型的截面图,下面是等腰梯形,中间是长方形,上面是一个等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
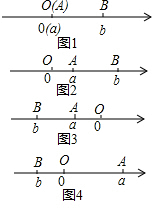 (1)阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a-b|,当A、B两点都不在原点时,
(1)阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a-b|,当A、B两点都不在原点时,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
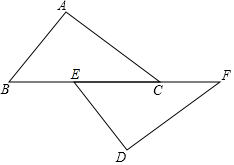 如图,已知点B、E、C、F在一条直线上,AC∥DE,AC=DE,∠A=∠D.
如图,已知点B、E、C、F在一条直线上,AC∥DE,AC=DE,∠A=∠D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com